'취미/Programming'에 해당되는 글 14건
- 2022.09.22 [Github] Github SSH 연결 완벽 가이드
- 2022.05.30 Telegram bot을 활용한 코드 실행이 끝나면 핸드폰으로 메시지 보내기
- 2021.09.08 opencv SimpleBlobDetector, blob size 정리
- 2021.09.06 Ubuntu TensorFlow(2.6) GPU 설치
- 2021.06.16 Matlab과 Python에서의 image 좌표축 한번에 정리!
- 2021.06.11 Ubuntu setup (Linux setup)
- 2021.03.24 [Vim] Linux 상에서의 Not an editor command: ^M 문제
- 2020.10.28 Python(anaconda) Vim intagration 2
- 2020.05.06 Multi Layer Perceptron (MLP) 1
- 2019.11.13 [GitHub] 3. GUI Git: GitHub Desktop, Sourcetree, GitKraken
들어가며
안전한 보안을 위한 좋은 방법 중 하나는 Two Factor Authentication (2FA)를 계정에 설정해두는 것이다. 사이드마다 다른 비빌먼호 생성, 주기적인 비밀번호 변경보다 훨씬 쉽게 보안 수준을 높게 유지할 수 있다. 그런데 github에 2FA 인증을 설정해두면 서드파티 앱이나 shell에 있는 git 에서 remote repository (remote)에 접근을 하기 어려워진다. 또한 지난 2021년 8월 13일부로 github 계정을 사용한 remote 접근이 완전히 차단되어서 더이상 단순히 비밀번호를 입력해서 접근하기가 어려워졌다. 때문에 아래와 같은 방법을 통해 remote에 접근 할 수 있다.
1. Token 발급 : sub-password의 역할을 하는 token을 발급받아 비밀번호 대용으로 쓰는 방식으로, 각 token 마다 유효기간, 권한등을 설정할 수 있다. 기존의 github 계정 비빌번호를 사용하는 방법을 완전히 대체 가능하다.
2. OAuth : Open Authentication. 로컬 git, 서트파티앱에 github 로그인 정보를 제공하지 않고 github에 연결하게 해주는 인증방식이다.
3. SSH : 이 글에서 다룰 내용으로 한번 설정만 제대로 한다면 편리하고 보안성도 좋다.
설정 난이도만 생각하면 Token을 발급받는 방법이 가장 쉽다. Token을 발급받아서 필요한 권한을 준 뒤, 어딘가에 적어두고 remote를 연결할 때 사용하면 된다. 그러나 더 높은 보안과 편리성을 위해서는 SSH를 사용하는 것을 추천한다.
SSH 연결 특징
SSH는 Secure SHell의 약자이며 구체적인 SSH 통신 방법은 여기에서 다루지 않겠다. 대신, SSH 를 사용하면 어떤 것들이 필요하고, HTTPS를 사용하는 방식과는 어떻게 다른지 비교를 하겠다.
사용자 이름을 knowblesse, repository 이름을 myrepo라고 했을 때 HTTPS와 SSH에서 필요한 것은 아래와 같다.
| HTTPS | SSH | |
| remote repository 주소 | https://github.com/knowblesse/myrepo | git@github.com:knowblesse/myrepo.git |
| ID | knowblesse@gmail.com | X |
| PSW (Token) | ghp_********* | X |
| Public Key / Private Key | X | SHA256:e/*************** |
| (옵션) credential 저장 | git config credential.helper store git config --global user.name Knowblesse git config --global user.email knowblesse@gmail.com |
eval "$(ssh-agent -s)" ssh-add |
차이점 1 : remote 주소
SSH는 인증방식이 아니라 (보안 인증 프로토콜을 포함하고 있는) 통신 방식이다. 때문에 일반적으로 알고 있는 https로 시작하는 주소가 아닌 git@github.com 으로 시작하는 주소를 입력해야한다.
차이점 2 : 인증
SSH에서는 public key와 private key, 두 가지 파일을 사용하는 공개키 암호화 방식을 기본으로 택하고 있다. 처음에 key 생성기를 사용해서 서로 매치가 되는 public key와 private key를 생성하고, 인증을 원하는 곳에 public key를 제공하면 이후 접속시 private key를 이용해서 인증받을 수 있다.
차이점 3 : Credential 저장
token을 사용하는 HTTPS 방식에서는 credential.helper를 사용해서 token을 저장해둘 수 있다. SSH에서는 ssh-agent를 사용해 credential을 저장한다.
SSH 연결 설정
SSH 연결 설정 순서는 다음과 같다.
1. SSH 키가 없는 경우 : SSH 키 생성
2. Github에 SSH 등록
3. local repository에 SSH 기반 remote 주소 등록
4. ssh-agent 셋업 및 연결 방법
1. SSH 키 생성
SSH 키 생성은 다양한 프로그램이 지원하고 있는데, Window와 Linux 모두 기본으로 설치되어있는 ssh-keygen을 사용하는 방법이 가장 보편적이다.
먼저 기존에 생성해둔 ssh키가 없는지 간단히 확인한다.
Window ("C:\Users\Knowblesse") 와 Linux ("\home\Knowblesse") 의 유저폴더 안에 ".ssh" 라는 명칭의 폴더 안에 .pub로 끝나는 파일이 있는지 확인해보면 된다. 키 생성을 한번도 안한경우 폴더 자체가 없을 것이다.
Window cmd나 Linux shell에서 다음과 같이 ssh-keygen을 실행하자.
> ssh-agent -t ed25519ssh-agent는 기본 옵션으로 rsa key pair를 만드는데 최신 방식은 ed25519라고 한다. 기본 옵션으로 키를 생성하려면 "ssh-agent"만 실행하면 된다.
이후 파일을 저장할 위치를 묻는데 default 위치를 그대로 사용해야지, 다른 곳에 저장을 했다가는 추가로 key 위치를 입력해주는 작업을 해야한다. 가능하면 ~/.ssh 폴더 안에 생성하도록 그대로 두자.
> ssh-keygen -t ed25519
Generating public/private ed25519 key pair.
Enter file in which to save the key (C:\Users\Knowblesse/.ssh/id_ed25519):다음으로는 password를 묻는다.
> ssh-keygen -t ed25519
Generating public/private ed25519 key pair.
Enter file in which to save the key (C:\Users\Knowblesse/.ssh/id_ed25519):
Enter passphrase (empty for nopassphrase):이 passphrase는 private key를 한번 더 암호화 하는데에 사용된다. private key에도 암호를 걸어두는 것을 적극 권장한다.
Q. 왜 passphrase를 설정하나요?
A. 행여나 private key가 노출되었을때를 방지하기 위함입니다. 실질적인 보안은 사실 public/private key 쌍이 담당하고 있기에 passphrase를 복잡하게 설정할 필요는 없습니다. 때문에 명칭도 password가 아니라 phrase 입니다.
private key에 암호설정 과정을 마치면, 아래와 같은 출력 메시지 후에 public key와 private key가 생성된다.

.pub 확장자를 가진 파일이 public key, 아무런 확장자가 없는 파일이 private key 이다.
생성된 두 파일은 텍스트 편집기로 열 수 있는 plain text 파일이며 private key는 절대 인터넷 상에 노출이 되면 안된다.
Q. 어차피 private key는 public key와 인증을 거치는 과정 중에서 인터넷 상에 노출되지 않나요?
A. SSH 인증에 사용하는 비대칭 공개키 암호화 방식은 1) 서버가 랜덤한 메시지를 호스트로 보내고, 2) 이를 받은 호스트는 private key로 암호화를 해서 다시 서버에게 보내고, 3) 암호화된 메시지를 받은 서버가 자신이 가지고 있는 public key를 사용해 복호화 한 뒤, 원래 보냈던 메시지와 비교하는 방식입니다. 때문에 private key는 인터넷 상에 절대 노출되지 않습니다.
2. Github에 SSH 등록
생성한 public키는 Github에 등록할 수 있다.

새로운 SSH 키 등록 버튼을 누른 뒤, 텍스트 편집기로 .pub 파일을 열어서 내용을 붙여넣으면 된다.

3. local repository에 SSH 기반 remote 주소 등록
여기서부터 살짝 까다로워 진다.
3-1. 처음 repository를 생성하는 경우 (clone 하는 경우)
https 기반 주소가 아니라 아래처럼 SSH 기반 주소를 입력하면 끝난다.
> git clone git@github.com/knowblesse/myrepo
3-2. 기존에 생성된 repository를 변경하는 경우
remote에 연결된 url 을 SSH 형식으로 수정하는 작업이 필요하다.
> git remote
origin먼저 git remote 커맨드로 어떤 remote 와 연결되어있는지 확인한다. 위의 예시에서는 origin만 연결되어 있다.
추가로 아래 커맨드를 사용하면 origin의 url을 볼 수 있다.
> git remote get-url origin
https://github.com/knowblesse/myrepo.giturl의 변경은 set-url을 사용하면 된다.
> git remote set-url origin git@github.com:knowblesse/myrepo.git형식에 주의하자
git@github.com:knowblesse/myrepo.git
Q. 여러 개의 SSH key를 사용할 경우에는 어떻게 하죠? 어떤 key를 쓰라고 지정할 수는 없나요?
A. ~/.ssh 폴더 안에 config 파일을 만들어서 어느 사이트에 연결할 때 어떤 key 파일을 사용할지 정해줄 수 있습니다. 이 방법 외의 다른 방법도 있지만, git command 안에서 "어떤 key 파일을 써라" 라고 명시적으로 알려주는 방식은 없는 것으로 알고 있습니다. config 파일을 생성하는 방법은 아래 접은 글을 참고해 주세요.
config 파일 만드는 법
open SSH 에서 사용하는 config 파일은 여러 요소로 구성되어 있으나, 복수의 key를 사용하기 위한 목적이면 Host, HostName, IdentityFile 3개의 키워드만 사용하면 된다. 구체적인 작성법은 다음 사이트를 참고하자.
https://www.ssh.com/academy/ssh/config
SSH config file syntax and how-tos for configuring the OpenSSH client
SSH config file syntax and how-tos for configuring the OpenSSH client
www.ssh.com
config 파일을 사용해서 복수의 key를 사용하는 원리는 Host의 alias 생성이 가능하다는 점을 이용하는 것이다.
git@github.com:knowblesse/myrepo.git
위의 주소에서 git 은 사용자명(knowblesse가 아니다!), github.com 은 Host의 위치, knowblesse/myrepo.git은 호스트 서버 내의 내 remote의 위치이다(정확히는 remote 정보를 담고 있는 git 파일).
중요한 점은 github.com 이 실제 주소가 아니라 Host의 이름 이라는 것인데 open SSH는 config 파일에서 해당 이름을 가진 Host가 없으면 이를 실제 Host 주소로 사용해서 실제 github.com과 통신을 시작한다.
반면, Host를 지정해주고 실제 Host의 주소를 config 파일에 명시하면 다른 형태로 접속이 가능하다.
Host myhub
HostName github.com예를들어, 위와 같이 config 파일을 설정해주면 이후 github.com을 입력하지 않고 단순히 아래처럼 입력할 수 있다.
git@myhub:knowblesse/myrepo.git
주의점은 HostName이 alias가 아니라 Host가 alias이다. HostName은 실제 주소다!
또한 config 파일에서는 각 host 마다 사용할 IdentityFile의 위치를 지정할 수 있다.
여기까지 설명을 하면 이미 눈치를 챘을 것이다. IdentityFile만 다르게 지정한 alias를 여러개 만들어 두면 remote의 set-url을 진행할 때 사용하는 alias에 따라 다른 key 파일을 사용하도록 할 수 있다.
다음은 account1_private 과 account2_private key 파일을 사용하는 config 파일의 예시이다.
#keyfile 1
Host account1
HostName github.com
IdentityFile ~/.ssh/account1_private
#keyfile 2
Host account2
HostName github.com
IdentityFile ~/.ssh/account2_private이후 git remote set-url 함수를 사용해서 repo 마다 remote의 주소를 설정해주어야 한다.
예를 들어 account1_private key 파일을 repo1에 사용하려면 아래와 같이 url을 변경한다.
> git remote set-url origin git@account1:knowblesse/repo1.git4. ssh-agent 셋업 및 연결 방법
여기까지 설정을 완료했고, key 파일이 기본 위치인 ~/.ssh 안에 들어있다면 정상적으로 remote와 연결이 될 것이다. 그러나 매번 passphrase를 물어본다는 단점이 있다. 이를 해결하는 방법은 ssh-agent를 사용해서 잠시동안 passphrase를 저장해두는 것이다. 이 경우 한동안 passphrase 없이 SSH 통신을 할 수 있다. 마치 credential.helper 를 사용해서 token을 저장해두는 것과 동일하다.
순서는 두 과정을 거치는데, 1)ssh-agent를 실행하고, 2) ssh-add를 통한 key 등록이다.
Linux
> eval `ssh-agent -s`
Agent pid 12345
> ssh-addWindows (PowerShell)
> Set-Service ssh-agent -StartupType Manual
> Start-Service ssh-agent
> ssh-addQ. 왜 그냥 ssh-gent를 실행하면 안되고 꼭 eval 함수 사용해서 실행해야하죠?
A. eval을 쓰지 않고 ssh-agent 명령을 실행해도 ssh-agent 프로세스는 정상적으로 시작된다. 그런데 그 이후에 ssh-add가 정상작동하지 않는다. 그 이유는 ssh-add가 SSH 소켓에 대한 정보를 필요로 하기 때문이다.
ssh-agent 명령을 실행하면 다음과 같은 출력이 나온다.
> ssh-agent -s
SSH_AUTH_SOCK=/tmp/ssh-XXXXXXmj93qJ/agent.36991;
export SSH_AUTH_SOCK;
SSH_AGENT_PID=36992;
export SSH_AGENT_PID;
pid 36992;
눈치 챘겠지만, ssh-agent 명령은 ssh-add 에게 매번 긴 SSH_AUTH_SOCK에 해당하는 값을 전달해주지 않도록 SSH 소켓과 ssh-agent 관련 정보를 bash 코드로 출력한다. 때문에 출력 텍스트를 그대로 코드처럼 실행시키는 eval 함수를 사용하여 ssh-agent를 실행하면, ssh-agent의 출력결과인 소켓과 pid 설정을 자동으로 할 수 있다!
때문에 굳이 eval을 쓰고 싶지 않다면, ssh-agent를 돌려서 나온 소켓과 pid 정보를 아래와 같이 변수로 입력해주면 된다.
> SSH_AUTH_SOCK=/tmp/ssh-XXXXXXmj93qJ/agent.36991
> SSH_AGENT_PID=36992
> ssh-add
Q. 왜 윈도우에서는 서비스 시작 방법을 바꾸나요?
A. Startup Type 이 Manual이 아니면 수동 시작이 안되는 것 같다. 윈도우는 UI가 잘 되어 있으니 수동시작을 하지말고 시작시 자동 시작을 하게 하면 더 편할 것 같다.
마치며
SSH 설정이 단순하지는 않지만, 한번 설정만 해두면 높은 보안수준을 유지하며 쉽게 데이터 공유가 가능하다.
'취미 > Programming' 카테고리의 다른 글
| Telegram bot을 활용한 코드 실행이 끝나면 핸드폰으로 메시지 보내기 (0) | 2022.05.30 |
|---|---|
| opencv SimpleBlobDetector, blob size 정리 (0) | 2021.09.08 |
| Ubuntu TensorFlow(2.6) GPU 설치 (0) | 2021.09.06 |
| Matlab과 Python에서의 image 좌표축 한번에 정리! (0) | 2021.06.16 |
| Ubuntu setup (Linux setup) (0) | 2021.06.11 |

사용 후 꼭 레버를 올려주세요
연구실에 사비로 캡슐 커피머신을 비치해두었는데, 공유지의 비극으로 관리의 문제가 심각해진 적이 있었다. 캡슐을 사용하고 레버를 올리지 않는 경우 캡슐이 그대로 기기안에 남는데, 기온이 높은 여름에는 따뜻하고 눅눅한, 곰팡이가 번식하기에 최적인 조건이 만들어진다. 특히 금요일 오후즈음 이런 상황이 발생하면 주말내내 커피머신은 곰팡이 배양기로써 그 역할을 충실히 수행한다. 월요일 아침에 커피를 마시기 위해 레버를 올리는 순간, 떨어지는 캡슐에 핀 곰팡이를 보게되면 결국 기기 분해 세척은 주인인 내 몫이 되었다.
다들 범행(?)을 부인하는 통에 전체 공지도 돌리고 사진처럼 Negative Punishment도 해봤으나 인간은 쉽사리 바뀌지 않는법. 결국 Raspberry Pi를 사용해 커피 머신 사용 중 동영상을 촬영하고, 2분내로 레버를 올린 경우 동영상은 삭제, 레버를 올리지 않은 경우는 동영상을 저장한 뒤, 내게 이메일로 노티를 주는 장치를 만들었다. (코드)
GitHub - knowblesse/BlueberryPi
Contribute to knowblesse/BlueberryPi development by creating an account on GitHub.
github.com
원래 계획은 범인의 커피 내리는 영상을 (이게 생각보다 우스꽝스럽다) 반복 재생시켜두려고 했으나, 매우 안타깝게도 높으신 분의 반복범행임이 밝혀져서 깔끔히 포기했다. 10개의 범행장면을 모은 뒤 '두근두근 범인 공개 상영회'를 연 것으로 만족했으며, 그냥 스스로 자주 확인을 하기로 했다.
코드 다 돌아가면 알려줘!
앞서 언급한 프로젝트를 진행하던 중 처음 겪은 불편함은 범인이 걸렸는지 확인하려면 직접 기기에 가서 파일 생성 여부를 체크해야 했다는 점이다. 터치스크린을 연결해두기는 했지만 매일 기기 체크하기가 귀찮아서 범인이 잡히면 이메일을 보내는 스크립트를 만들었는데, 이는 생각보다 단순하다. (코드) 구글, 네이버 등의 이메일 SMTP 서버를 사용해서 내 계정에서 내 이메일로 메일을 보내도록 설정하면 된다. 단점으로는 이메일 자체가 느리고, 내 핸드폰의 이메일 동기화 주기가 그렇게 짧지 않아서 즉각적인 메일 확인이 어렵다는 점이다. 물론 커피 머신 범인을 확인하는게 급한 문제는 아니었기에 만족하면서 사용했다.
그러나 다른 컴퓨터에서 코드를 돌리고 실행이 완료되거나, 문제가 발생하면 알려주는 기능은 커피 머신보다는 급한일이다. 더욱이 이메일로 보내는 경우 다른 중요치 않은 이메일에 섞여서 묻힐 수 있다. 때문에 기존 메신저 앱들 중 편리한 API 구성을 제공하는 것이 없나 검색하다가 Telegram의 bot을 활용하는 방법이 군더더기 없이 제일 깔끔해서 이를 소개하려고 한다.
Why Telegram?
사실 텔레그램하면 지난 몇 년간 언론을 달군 사건이 생각나서 설치 자체가 조금 꺼려지기는 했으나 군더더기 없이 깔끔하다는 말에 이를 택했다. 카카오톡이 추가앱 설치도 필요없어서 가장 유력한 후보였으나, 플러스친구, 로그인 등 각종 기능 등과 같이 묶여있어서 그런지 너무 복잡해 반쯤 만들다가 포기했다. 또한 정확히 "코드 다 돌아가면 알려줘!"의 목적에 부합하는 bot 기능을 가지고 있기에 Telegram을 택했다.
How to
먼저 핸드폰에 Telegram 앱을 설치하고 계정을 만든다. 연락처 동기화를 자꾸 요구하는데 그닥 메인 메신저로 쓸 생각이 없어서 차단했다.
1. 먼저 BotFather를 사용자에서 찾아서 새로운 bot을 만든다.

2. BotFather 와 대화를 시작하고 /newbot 을 보내면 이름과 id를 물어보는 작업을 거쳐 bot을 만들어준다.
이름은 그렇다쳐도 id는 중복이 있으면 안되는 점이 조금 귀찮다.
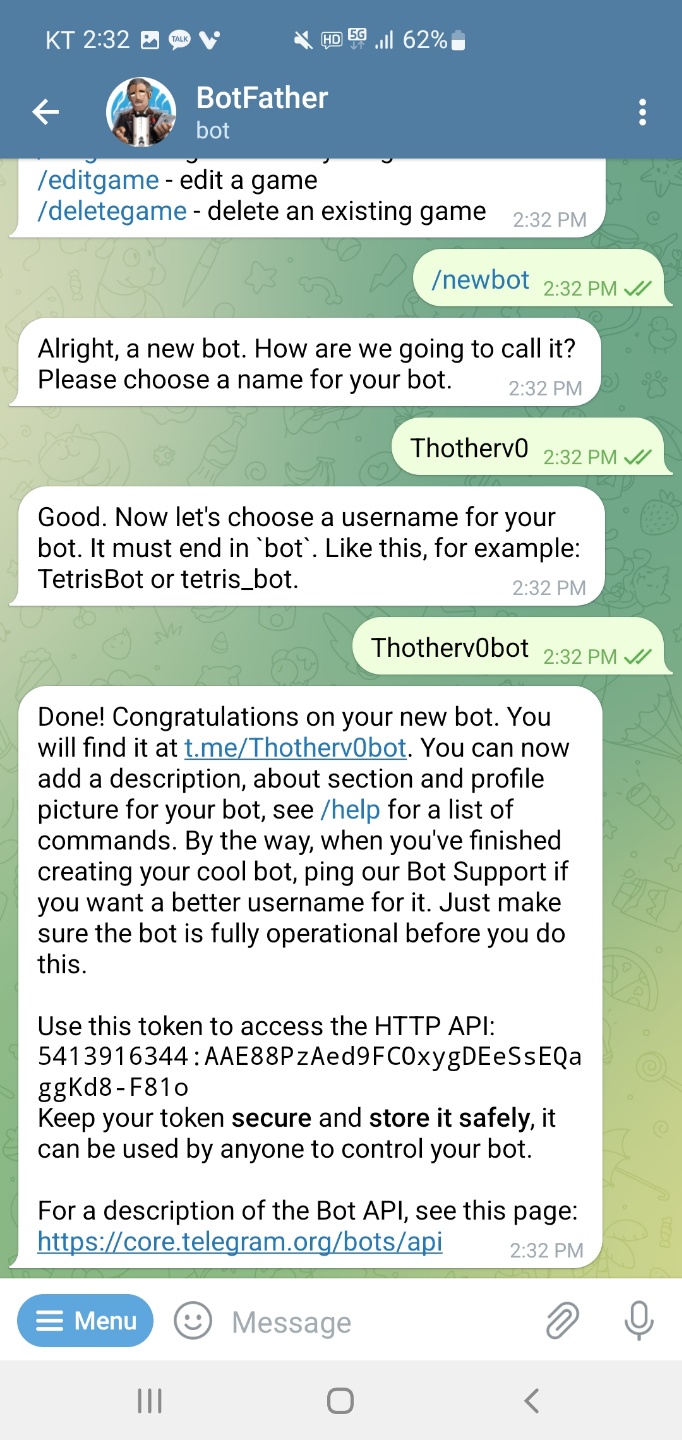
해당 과정을 완료하면 HTTP access token을 발급해준다. 이 정보가 있어야 해당 봇을 통해 본인의 핸드폰으로 메시지를 보낼 수 있다. 함께 알려주는 api 사이트에 들어가면 생각보다 많은 기능을 지원한다는 것을 확인가능하다. 하지만 우리는 단 세 가지 함수만 사용할 예정임으로 굳이 들어가볼 필요는 없다.
3. HTTP 호출을 통해서 bot 생성여부를 체크한다.
HTTP GET, POST 등의 method 테스트를 위해서 예전에 Postman이라는 프로그램을 배웠고, 이런 프로젝트마다 디버깅 목적으로 사용하는데 간단한 튜토리얼임으로 기본 웹브라우저를 사용해서 설명하려한다. 별개로 Postman 프로그램이 꽤 유용하니 시간되면 꼭 살펴보시길.
Postman API Platform | Sign Up for Free
Postman is an API platform for building and using APIs. Postman simplifies each step of the API lifecycle and streamlines collaboration so you can create better APIs—faster.
www.postman.com
웹 브라우저(본인은 파이어폭스) 주소창에 아래와 같이 입력을 하면 생성한 bot과 연결이 잘 되는지 확인할 수 있다.
https://api.telegram.org/bot아까발급받은토큰/getMe
# 예시 : https://api.telegram.org/bot5413916344:AAE88PzAed9FCOxygDEeSsEQaggKd8-F81o/getMe문제가 없다면 아래와 같은 ok 사인을 받을 수 있다.
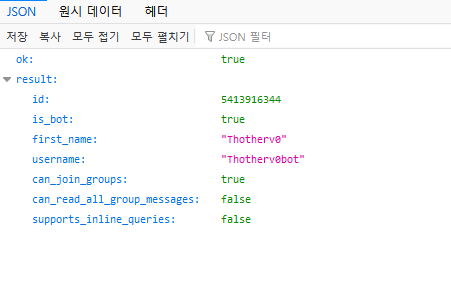
4. bot에게 말을 걸자.

핸드폰으로 돌아가서 bot 생성시 두번째로 입력했던 id로 사용자를 검색하면 해당 bot을 찾을 수 있다. 이 bot과 대화를 시작하고, 메시지 하나를 보내두자. bot은 자체적으로 사용자에게 최초로 메시지를 보낼 수 없다. (스팸방지)
5. 생성된 대화방의 id를 불러온다.
https://api.telegram.org/bot아까발급받은토큰/getUpdates
# 예시 : https://api.telegram.org/bot5413916344:AAE88PzAed9FCOxygDEeSsEQaggKd8-F81o/getUpdates다시 브라우저로 돌아가서 위 주소로 간다. 성공적으로 호출이 되면 아래와 같이 대화내용을 불러올 수 있을 것이다.

getMe를 호출하기 이전에 먼저 대화부터 보내고 나중에 getUpdates를 호출했더니 앞선 대화가 누락되는 문제를 확인했다. (첨부한 이미지에서도 보낸 메시지는 hi there부터 시작하는데 불러온 대화내용은 그뒤에 보냈던 "ㅁㅁ"만 보인다.) 다시 메시지를 보내면 getUpdates에서 잘 보이는 것 같으니 큰 문제는 아닌 것 같다.
이렇게 성공적으로 대화를 받으면, id 값을 확인한다. 이 경우 55201이다.
6. http request를 통해 메시지를 보내자
모든 과정이 끝났다. 메시지를 보내는 함수는 sendMessage이며 아래와 같이 사용하면 된다.
https://api.telegram.org/bot아까발급받은토큰/sendMessage?chat_id=아이디&text=보낼메시지
# 예시 : https://api.telegram.org/bot5413916344:AAE88PzAed9FCOxygDEeSsEQaggKd8-F81o/sendMessage?chat_id=55201&text=Code Finished
python의 경우는 request 패키지를 설치한 후, 아래의 함수를 넣어주면 된다.
import requests
requests.get('https://api.telegram.org/bot5413916344:AAE88PzAed9FCOxygDEeSsEQaggKd8-F81o/sendMessage?chat_id=55201&text=Code Finished')text 뒤에 코드가 돌아갔다는 정보 외에 시간, 에러가 발생한 경우 그 에러 내용등의 첨부가 가능하다.
무엇보다 모든 과정이 핸드폰으로 진행이 가능하며, access token, 본인 telegram 대화방의 id, 단 두 개 정보만 확인되면 메시지를 바로 보낼 수 있다.
주의
github가 금광산이라는 말을 들은 적이 있다. 특히 요 얼마전에는 아마존 AWS에 스타트업에서 사용하는 기업용 계정 access token을 실수로 github에 그대로 올렸다가 수 십억에 달하는 사용료가 부과되었다는 뉴스가 나온적이 있다. 모르는 사람은 바보 같다고 생각하겠지만 평상시 버전 관리 프로그램을 쓰는 습관 때문에 나도 충분히 할법한 실수라고 생각한다. Telegram bot token으로는 그러한 짓을 할 수 없겠지만 access token이 어딘가에 공개가 되지 않도록 꼭 주의하자. 본 예시에 사용된 계정은 전부 비활성화 처리를 완료했다.
'취미 > Programming' 카테고리의 다른 글
| [Github] Github SSH 연결 완벽 가이드 (0) | 2022.09.22 |
|---|---|
| opencv SimpleBlobDetector, blob size 정리 (0) | 2021.09.08 |
| Ubuntu TensorFlow(2.6) GPU 설치 (0) | 2021.09.06 |
| Matlab과 Python에서의 image 좌표축 한번에 정리! (0) | 2021.06.16 |
| Ubuntu setup (Linux setup) (0) | 2021.06.11 |
1. SimpleBlobDetector
parameter로 넣어준 조건에 따라 blob을 찾아줌.
알고리즘
- source image에 threshold를 적용.
- parameter에 넣은 minThreshold 값(포함)과 maxThreshold 값(불포함) 사이를 thresholdStep으로 나누어 각각의 threshold를 사용해서 binary image로 바꾼다. 처음부터 binary를 넣어주려는 경우 기본 파라미터에서는 minThreshold=50, maxThreshold=220, thresholdStep=10 으로 설정이 되어있기에 이를 만져주어야 한다.
binary image를 0과 255로 구성되도록 설정하고, minThreshold=253, maxThreshold=255, thresholdStep=1로 설정하면 최소한의 threshold 연산만 사용할 수 있다. - 각각의 binary image에 대해서 findContours 함수를 적용해서 center를 계산.
- 각각의 binary image에서 찾은 contour들을 하나로 묶어줌.
이때 minDistBetweenBlobs parameter를 사용한다. - 찾아낸 Contour를 사용해서 blob의 최종 center와 radius를 확정. 이를 keypoint로 return
예시코드
import cv2 as cv
parameter = cv.SimpleBlobDetector_Params()
parameter.filterByArea = True
parameter.filterByConvexity = True
parameter.filterByCircularity = True
parameter.filterByInertia = False
parameter.filterByColor = False
parameter.minArea = 500 # this value defines the minimum size of the blob
parameter.maxArea = 10000 # this value defines the maximum size of the blob
parameter.minDistBetweenBlobs = 1 # not used in binary image
parameter.minConvexity = 0.3
parameter.minCircularity = 0.3
detector = cv.SimpleBlobDetector_create(parameter)
detected_blob = detector.detect(denoised_mask)
print(len(detected_blob))2. keypoint size
keypoint는 pt 값과 size 값을 가지고 있는데 (다른 값들도 있지만 이 연산에서는 무의미한 것으로 추정) pt는 blob center의 x, y 좌표를 의미하지만 도무지 size에 대한 이야기가 없다.
내가 원하는 정보는 찾아낸 blob의 크기 (이를 둘러쌀 수 있는 최소한의 원의 반지름 이라던가 실제 blob의 픽셀 수라던가...)인데 나오는 size 값은 blob의 모양에 따라서 제각각이다.

4번째 스텝인 "찾아낸 Contour를 사용해서 blob의 최종 center와 radius를 확정." 에서 대체 무슨일이 일어나는 것이길래 이런 값이 출력되는지 모르겠다. 원 같은 경우는 그나마 비슷하긴 하지만 실제 위의 그림에서 볼 수 있듯이 지름 100px짜리 원의 blob 크기는 99.0151로 나온다. 여러 contour 들을 합치는 알고리즘을 들여다봐야 알겠지만 SimpleBlobDetector가 return하는 keypoint의 값만 사용해서 실제 blob의 크기를 알아낼 방법은 없는 것으로 보인다.
3. parameter의 minArea / maxArea
한 가지 주목할 점은 parameter로 사용하는 minArea / maxArea의 경우는 실제 blob으로 잡힌 object의 크기를 비교한다는 것이다. 한 변의 길이가 100px인 정사각형에 대한 keypoint의 size 값은 111.8034이지만 filterByArea 옵션을 켜고 minArea를 10000(100 * 100)으로 잡으면 정사각형을 찾지만, 10001을 사용하는 경우 정사각형을 찾지 못한다. circle의 경우는 사용한 radius를 사용해 수학적으로 계산한 넓이와 10 이하로 차이가 나는 것으로 보아 실제 pixel 수를 기준으로 filter 하는 것으로 보인다.
4. findContours 함수를 사용한 정확한 blob detection
때문에 내부에서 찾아낸 blob의 정확한 사이즈를 뽑아낼 수 있을 것이라고 기대했으나 실패했다.
사실 실제 4단계 step 중에서 사용하는 부분이 두 번째 step 뿐이기에 이쯤되면 그냥 findContous 함수를 써서 raw level에서 처리하는 것이 더 나을 것으로 보인다.
cnt = cv.findContours(binary_image, cv.RETR_EXTERNAL, cv.CHAIN_APPROX_SIMPLE)[0]
# Some basic features of the contour object
(x,y), radius = cv.minEnclosingCircle(k)
rect = cv.minAreaRect(k) # ((center x, center y), (width, height), rotation)
size = cv.contourArea(k)뽑아내야 하는 blob의 수를 알고 있다면 area, 둘러싸는 직사각형의 가로 세로 사이즈 등등의 값을 얻은 뒤 단계적으로 filter를 적용하는 방법도 사용할 수 있다.
'취미 > Programming' 카테고리의 다른 글
| [Github] Github SSH 연결 완벽 가이드 (0) | 2022.09.22 |
|---|---|
| Telegram bot을 활용한 코드 실행이 끝나면 핸드폰으로 메시지 보내기 (0) | 2022.05.30 |
| Ubuntu TensorFlow(2.6) GPU 설치 (0) | 2021.09.06 |
| Matlab과 Python에서의 image 좌표축 한번에 정리! (0) | 2021.06.16 |
| Ubuntu setup (Linux setup) (0) | 2021.06.11 |
Google아 TF2.6이 나온지 언젠데 아직도 install 페이지에 TF2.4 설치방법이 있더라.
일 안하니?
망할 파이썬을 쓰다보면 인생의 교훈을 한가지 얻을 수 있다.
새로운 것 나왔다고 바로 쓰지말고 나온지 좀 된 것을 쓰자.
그런데 기왕 셋업하는 김에 좀 최신 것을 쓰려고 했다가 시간을 엄청 날렸다. TensorFlow 자체 documentation 은 금방금방 업데이트를 해주는데 설치방법은 왜 여전히 그대로인지... 내가 설치할 당시에는 2.5 기준으로 documentation이 나와있었는데 2.5는 CUDA 11.2 버전이 필요하고, 홈페이지에 나와있는 설치방법은 11.0을 기준으로 나와있어서 그대로 설치했다가는 'tf 2.5 에서는 cuda 11.2 버전이 필요합니다' 에러를 낸다.
문제는 이 cuda 11.2가 그당시 완성이 덜 되어있어서 몇몇 라이브러리가 없었는데 이 때문에 수동으로 라이브러리를 다운받아 이름을 변경하여 넣어야 돌아갔다. 세상에.
화난 개발자들이 올린 글들의 도움을 얻어 어찌저찌 설치를 했는데 왜 이 글을 쓰냐... apt-get autoclean과 apt-get autoremove 를 썼다가 수동으로 다운받아둔 라이브러리가 다 날아갔다. 이왕 다시 셋업 하는거 기록으로 남겨두자는 마음으로 글을 작성한다.
docker를 쓰는 쉬운 방법도 있다는 것 같지만 docker에 대한 필요성을 딱히 못 느끼기에 사용하지 않았다. 그래도 가상환경을 사용하지 않고 새로운 패키지를 까는 것을 죄악이니 꼭 conda는 사용하길 바란다.
0. tensorflow 2.6 설치
혹시 설치하지 않은 경우...
pip install tensorflow==2.61. NVIDIA GPU driver 설치
자기 그래픽 카드에 맞게 최신으로 설치.
https://www.nvidia.com/download/index.aspx?lang=en-us
Download Drivers | NVIDIA
www.nvidia.com
2. CUDA Toolkit 11.4 Update 1 (11.4.1) 설치
https://developer.nvidia.com/cuda-toolkit-archive
CUDA Toolkit Archive
Previous releases of the CUDA Toolkit, GPU Computing SDK, documentation and developer drivers can be found using the links below. Please select the release you want from the list below, and be sure to check www.nvidia.com/drivers for more recent production
developer.nvidia.com
콘솔에서 커맨드 실행전에 sudo 명령어를 사용하는 다른 명령을 사용해두는 것이 좋다.
안그러면 첫줄만 돌아가고 root password를 묻는 통에 둘째 라인부터 실행이 되지 않는다.
Ubuntu 18.04
wget https://developer.download.nvidia.com/compute/cuda/repos/ubuntu1804/x86_64/cuda-ubuntu1804.pin
sudo mv cuda-ubuntu1804.pin /etc/apt/preferences.d/cuda-repository-pin-600
wget https://developer.download.nvidia.com/compute/cuda/11.4.1/local_installers/cuda-repo-ubuntu1804-11-4-local_11.4.1-470.57.02-1_amd64.deb
sudo dpkg -i cuda-repo-ubuntu1804-11-4-local_11.4.1-470.57.02-1_amd64.deb
sudo apt-key add /var/cuda-repo-ubuntu1804-11-4-local/7fa2af80.pub
sudo apt-get update
sudo apt-get -y install cudaUbuntu 20.04
wget https://developer.download.nvidia.com/compute/cuda/repos/ubuntu2004/x86_64/cuda-ubuntu2004.pin
sudo mv cuda-ubuntu2004.pin /etc/apt/preferences.d/cuda-repository-pin-600
wget https://developer.download.nvidia.com/compute/cuda/11.4.1/local_installers/cuda-repo-ubuntu2004-11-4-local_11.4.1-470.57.02-1_amd64.deb
sudo dpkg -i cuda-repo-ubuntu2004-11-4-local_11.4.1-470.57.02-1_amd64.deb
sudo apt-key add /var/cuda-repo-ubuntu2004-11-4-local/7fa2af80.pub
sudo apt-get update
sudo apt-get -y install cuda3-1. cuDNN v8.2.2 for CUDA 11.4 다운
아래 사이트에서 cuDNN Library for Linux (x86_64)를 다운받으면 된다.
원래 Debian Package (dpkg)를 사용해서 설치하는 것이 제일 간단한데 이게 왜인지 실행이 제대로 되지 않는다.
혹시 시도를 해보려면 아래 링크에서 cuDNN Runtime Library for Ubuntu18.04 x86_64 (Deb)를 받으면 된다.
Ubuntu 20.04인 경우 해당 버전에 맞는 것을 받자. Developer 버전을 받지 않아도 된다.
아래 설치는 dpkg가 아닌 library를 통째로 받은 것을 전제로 진행할 것이다.
https://developer.nvidia.com/rdp/cudnn-archive
cuDNN Archive
NVIDIA cuDNN is a GPU-accelerated library of primitives for deep neural networks.
developer.nvidia.com
3-2. cuDNN v8.2.2 for CUDA 11.4 설치
https://docs.nvidia.com/deeplearning/cudnn/install-guide/index.html
Installation Guide :: NVIDIA Deep Learning cuDNN Documentation
The NVIDIA® CUDA® Deep Neural Network library™ (cuDNN) is a GPU-accelerated library of primitives for deep neural networks. cuDNN provides highly tuned implementations for standard routines such as forward and backward convolution, pooling, normalizati
docs.nvidia.com
위 링크에서 자세한 설치 방법을 알 수 있으나, 아래에 간략히 요약하겠다.
받은 파일은 .tgz 확장자로 tar.gz 파일이다. 내장 파일탐색기 nautilus로도 압축을 풀 수 있고, 터미널에서 tar -xzvf 다운받은파일명 으로 풀 수 있다.
내장 파일탐색기로 푸는 것이 쉬우니 그 방법을 추천한다.
tar 명령어로 푸는 방법은 아래와 같다.
tar -xzvf cudnn-11.4-linux-x64-v8.2.2.26.tgz참고로, xzvf는 extract, gzip, verbosely list files processed, file 의 약자다.
다음으로 라이브러리를 CUDA Toolkit이 찾을 수 있는 장소에 넣어주어야 한다.
일반적으로 이는 /usr/local/cuda 폴더이며, 앞서 CUDA Toolkit을 설치하면 자동으로 생성되었을 것이다.
일단 터미널을 열고 압축을 풀어서 나온 cuda 폴더가 보이는 위치까지 간 뒤 아래 명령을 실행한다. 두 번째 명령이 파일이 많아서 시간이 조금 걸린다.
sudo cp cuda/include/cudnn*.h /usr/local/cuda/include
sudo cp -P cuda/lib64/libcudnn* /usr/local/cuda/lib64
sudo chmod a+r /usr/local/cuda/include/cudnn*.h /usr/local/cuda/lib64/libcudnn*4. 설치 종합
tensorflow v2.6 : tensorflow
CUDA Toolkit v 11.4.1 : CUDA 그 자체이다.
cuDNN v8.2.2 : library로 tensorflow 사용시 dynamic library 문제가 발생했다고 하면 이 친구가 문제인 것.
꼭 CUDA Toolkit은 cuDNN보다 먼저 설치해야 한다.
5. 확인
python에서 아래 코드로 GPU 사용을 확인해보자.
import tensorflow as tf
if tf.config.list_physical_devices('GPU'):
print('TF is using GPU')
else:
print('TF is NOT using GPU')
실행시 Information, Warning, Error로 로그가 나오는데, E만 없어도 대체로 정상작동하더라.

꼭 GPU로 돌아가는지 확인을 해보고 실행을 하자!
감사는 댓글이나 커피로 표현해주시면 감사히 받겠습니다.
'취미 > Programming' 카테고리의 다른 글
| Telegram bot을 활용한 코드 실행이 끝나면 핸드폰으로 메시지 보내기 (0) | 2022.05.30 |
|---|---|
| opencv SimpleBlobDetector, blob size 정리 (0) | 2021.09.08 |
| Matlab과 Python에서의 image 좌표축 한번에 정리! (0) | 2021.06.16 |
| Ubuntu setup (Linux setup) (0) | 2021.06.11 |
| [Vim] Linux 상에서의 Not an editor command: ^M 문제 (0) | 2021.03.24 |
서론
Matlab이든 Python이든 image 처리를 할때 좌표축 때문에 머리가 아파오는 경우가 꼭 생긴다. 바로 일반적인 좌표계인 x,y 기준으로 위치를 잡을지, image도 array의 일종이니 row, col 기준으로 위치를 잡을지 생각해야 하는 시점이다. 사실 정말 단순한 문제인데 의외로 헷갈리고 각도라도 계산해야 하는 시점이 생기면 지옥이 펼쳐진다. 이 글은 매번 image 처리 파트를 할 때마다 좌표축을 헷갈리는 멍청한 본인을 한번에 이해시키기 위해서 쓰는 글이다.
Rule #1

Matlab, Python, opencv, 캡쳐 프로그램, 지금까지 써본 모든 이미지 관련 프로그램들은 전부 이미지를 세 가지 형태중 하나의 형태로 사용한다. 그 이외의 형태는 아직까지 한번도 본적이 없다. 정확하게 말하자면 데이터 자체는 좌측과 같이 가지고 있고(실제 메모리에서의 구조보다는 indexing 기준), 사용자와 interaction을 해야하는 경우, 즉 마우스로 클릭을 하거나, line을 plot 하거나, figure의 현재 위치를 알려주거나 하는 경우는 중간이나 우측의 형태로 표기한다.
좌표축이 헷갈리는 가장 큰 원인은 개인적으로 데이터 입출력 형태가 두 가지가 있기 때문이라고 생각한다. indexing은 좌측, 입출력은 무조건 중간과 우측 중 하나의 형태만 취하면 그나마 혼동의 여지가 없겠으나, 입출력 형태가 2개가 있어서 혼란이 시작된다. 게다가 중간의 형태는 좌측의 형태와 정확히 일치하고 두 좌표값만 서로 바꾼 형태라 자칫 잘못하면 indexing을 method 1 방식으로 하게 되거나, method 1 방식으로 선을 그어주어야 하는데 indexing 하듯이 값을 넣을 수 있다.
가능한 모든 상황에서 테스트 해보면서 언제 어떤 식으로 좌표축이 표시되는지 확인해서 아래 정리해보았다.
사용하는 좌표축 형태 정리
| Matlab R2020a | Python 3.7.3 (matplotlib=3.1.0) |
|
| Indexing | indexing | indexing |
| Method 1 (reversed Y axis) | imshow, imagesc | imshow figure, object position |
| Method 2 (normal axis) | figure, object position plot, scatter 등 일반적인 graphic |
plot, scatter 등 일반적인 graphic |
| 현재 Method를 따름 | ginput, drawline | ginput |
Indexing
모든 경우에서 indexing을 하는 경우는 일반적인 array의 row, col 방식을 따르기에 가장 단순하다.
예를 들어 가장 최상단 좌측 픽셀을 검은색으로 만들고 싶으면 Matlab과 Python 각각 아래와 같이 입력하면 된다.
img(1,1,:) = 0 % Matlab
img[0,0,:] = 0 # PythonPosition Input
Matlab과 Python 모두 axis 상에서 마우스로 위치를 찍는 경우는 직관적으로 현재 axis의 상태를 그대로 따라 값을 저장해준다. 예를들어 imshow로 그림을 그려둔 상태에서 ginput을 실행하면 reversed Y axis 상태로 값을 기록한다. 반대로 plot 함수로 일반적인 cartesian 좌표계 상태라면 ginput 함수는 normal axis 상태로 값을 기록한다. 그러나 둘다 x, y 기준이지 row,col 기준이 아님을 기억하자.
Object Position(중요)
같은 기능에 대해서 여기서 Matlab과 Python, 그리고 다른 프로그램의 행동이 나뉘는 것 같다.
Python은 FigureManager의 geometry 속성 조절을 통해 window의 위치를 조정할 때 여타 image 처리에 사용되는 axis와 똑같이 reversed Y axis의 Method 1번 방식을 사용하는 반면, Matlab의 경우 Method 2 방식으로 figure window 의 position을 설정할 때 좌측 하단 구석이 원점이 된다.
GUI 개발을 할 때도 똑같은 형식으로 작동을 하는데, Matlab의 appdesigner를 사용하거나 ui가 붙는 object(button 등)를 만드는 경우 좌측 하단이 원점이 되는 Method 2 방식을 쓴다. Python으로는 GUI 개발을 해보지 않아서 확실히는 모르나 급히 PyQt5 관련 문서를 찾아보니 좌측 상단이 원점이 되는 Method 1 방식을 쓰는 것으로 보아 두 프로그램 모두 window position을 표기하는 방식과 동일하게 가는 것 같다.

결론
결론적으로 이미지 데이터 입/출력은 무조건 Method 1 방법, Position과 관련된 경우는 사용 언어에 따라 체크를 하고 넘어가는 식으로 규칙을 생각해두는 것이 좋다. 위치 데이터를 저장할 때는 나중에 저장한 위치를 다시 표시할 것을 대비해서 Method 1의 방법으로 저장하는 것이 가장 편하지만 저장한 위치로 image array를 자르거나 하는 복잡한 작업을 할 때 일이 더 복잡해질 수 있다. 본인은 그래서 무조건 데이터 저장은 row, col 기준으로 저장을 하고 필요한 경우에만 x,y로 입출력을 하려고 한다.
나중에 추가할 내용
flipud 한 뒤 set('YDir', 'normal')
'취미 > Programming' 카테고리의 다른 글
| opencv SimpleBlobDetector, blob size 정리 (0) | 2021.09.08 |
|---|---|
| Ubuntu TensorFlow(2.6) GPU 설치 (0) | 2021.09.06 |
| Ubuntu setup (Linux setup) (0) | 2021.06.11 |
| [Vim] Linux 상에서의 Not an editor command: ^M 문제 (0) | 2021.03.24 |
| Python(anaconda) Vim intagration (2) | 2020.10.28 |
서론
당신이 처음으로 Windows를 쓰던 날들을 기억하는가? 그저 어디를 어떻게 클릭해야 게임이 시작되는지만 알고 있다가 삭제된 파일을 휴지통에서 찾아오는 방법, Alt 키를 누르고 드래그 하면 바로가기가 생긴다는 사실 등을 배우게 되었을 것이다. 더 나아가서 Ctrl+Alt+Del 을 눌러 작업관리자를 불러와 먹통된 프로세스를 강제종료하거나 프록시 설정, 레지스트리 편집, 고정IP 설정 적용 등을 하나 둘 습득하게 된다. 물론 이러한 과정을 학원이나 정규 교육을 통해서 배우는 사람도 있겠지만, 굳이 누가 시키지 않아도 컴퓨터와 함께 살게 되는 요즘에는 인터넷을 뒤지다 새로운 사실을 알게되거나 컴퓨터를 고치다가 자연히 배우게 되는 사실들이 더 많을 것 같다고 생각한다.
Ubuntu를 본격적으로 사용하기 시작한 이후 자연히 알고 있던 다양한 OS의 기능들을 새로 배워야 한다는 것이 정말 신선했다. 당장에 현재 프로세스를 확인하고 싶어서 Ctrl+Alt+Del을 눌렀다가 날 로그아웃 시키려고 하질 않나, explorer를 열려고 Win+e 를 누르면 아무 일도 일어나지 않질 않나... 정말 답답하고 짜증나는 순간을 빈번히 '겪으며 언젠가는 이것도 익숙해 지겠거니' 하며 참고 억지로 썼는데 이제는 딱히 불편함을 느끼지 않고 편안히 Ubuntu를 사용하고 있다.
한가지 안타까운 것은 특정한 목적 중심(예를 들어 서버 관리)이 아닌 보편적인 사용을 위한 Ubuntu 관련 교재가 부족했으며, 무엇을 모르는지 어디를 어디까지 알아야 하는지를 모르기 때문에 많은 시행착오를 겪었다는 점이다. (210615추가: 그나마 '리눅스 마스터' 자격증 준비 책이 가장 광범위하고 자세히 나와있기는 하다.) 하지만 관련 책이 없는 것을 이해하는 게, 나도 가끔 부모님께 Windows 사용법을 설명할 때 당혹스러운 감정을 자주 느끼기 때문이다. 스스로에게는 너무나 일상적으로 쓰는 기능들이기에 설명 없이 넘어가버리거나 어디를 얼마만큼 깊게 설명해야하는지 고민을 할 때가 자주 생긴다. 하나의 OS는 끝까지 파고들어가면 수천 페이지 책 한권이 나올텐데 이것을 언제 다 설명하랴...
이 글은 Ubuntu 새끼 사용자가 시행착오를 통해 배워나가는 과정을 적는 글이다.
권한
- 최상위 권한인 root와 그 이외의 권한이 있다.
- 윈도우에서 관리자 권한으로 실행하라고 하면 그냥 실행하듯이 쓰는 Ubuntu 환경에서는 무언가 작업을 하다가 "Permission Denied"가 뜨면 sudo 를 앞에 붙이고 실행하면 비밀번호를 입력하고 관리자 권한으로 실행이 가능하다.
- 단, 다수의 사용자가 쓰는 환경의 경우 할수 있는 작업이 제한될 수 있다.
- /etc/passwd 파일에 들어가면 해당 시스템 내부의 모든 사용자를 볼 수 있는데 거의 40번째 줄까지는 시스템이 알아서 만들어주는 사용자일 것이고 가장 아래 자신의 이름이 있을 것이다.
- 사실 이 파일은 이름 : 비밀번호 : 계정 id : 그룹 id : 설명 : 사용하는 shell 의 구조로 되어있다고 해서 '비밀번호!!!' 를 외치며 눈을 밝히고 들어갔으나 x 표시로 되어있다.
- 실제 비밀번호는 암호화 되어 (아마 hash?) /etc/shadow 안에 보관된다.
- 권한에는 읽기, 쓰기, 실행하기 3종류가 있으며, chmod 를 통해서 권한 변경이 가능하다.
파일 구조
- 모든 (심지어 외장하드도) 파일은 최상위 directory인 root에서 파생된다. 그나마 윈도우에서 가장 유사한 개념은 '내 컴퓨터'일까. 약어로는 /로 표현한다.
- 그리고 대부분의 작업파일이 존재하는 곳은 /home/사용자명 이다. 이 폴더 안에 바탕화면, 음악/사진/문서, 다운로드 등등의 폴더들이 위치한다. 약어로는 ~ 로 표현한다.
- root 바로 하위에는 정말 다양한 폴더들이 존재하는데 굳이 하나하나 탐색하진 않았고 천천히 필요가 생길때마다 들어가는 것이 좋다.
- bin : 각종 명령어 함수들이 들어가 있다.
- dev : 기기에 연결된 저장장치, 입력장치 들이 다 이곳에 있다. 장치관리자?
- mnt : 마운트 된 저장장치가 위치한다.
- root : 루트 권한을 얻어야 들어갈 수 있는데 별게 없어보인다.
- etc : 온갖 설정파일들이 위치한다. root 바로 하위 directory 중에서 가장 자주 들락거린 것 같다.
- home : 위에서 설명.
- media : 자동으로 마운트 된 저장장치가 위치한다.
- 이 이외의 폴더들은 한번도 들어가본 적이 없어서 잘 모르겠다.
파일 탐색 방법
- 윈도우의 explorer 처럼 기본으로 nautilus(Files) 라는 프로그램이 깔린다. 제법 편리해서 간간히 쓴다.
- 무엇보다 리눅스는 외부 저장장치, 심지어는 내장 하드를 전부 root 밑에 mount 시켜야 읽기/쓰기가 가능한데 이게 초심자에게는 어렵다. 하지만 nautilus를 사용하면 좌측 bar에 뜨는 아이콘 클릭만으로 저장장치를 /media에 mount 시킬 수 있다.
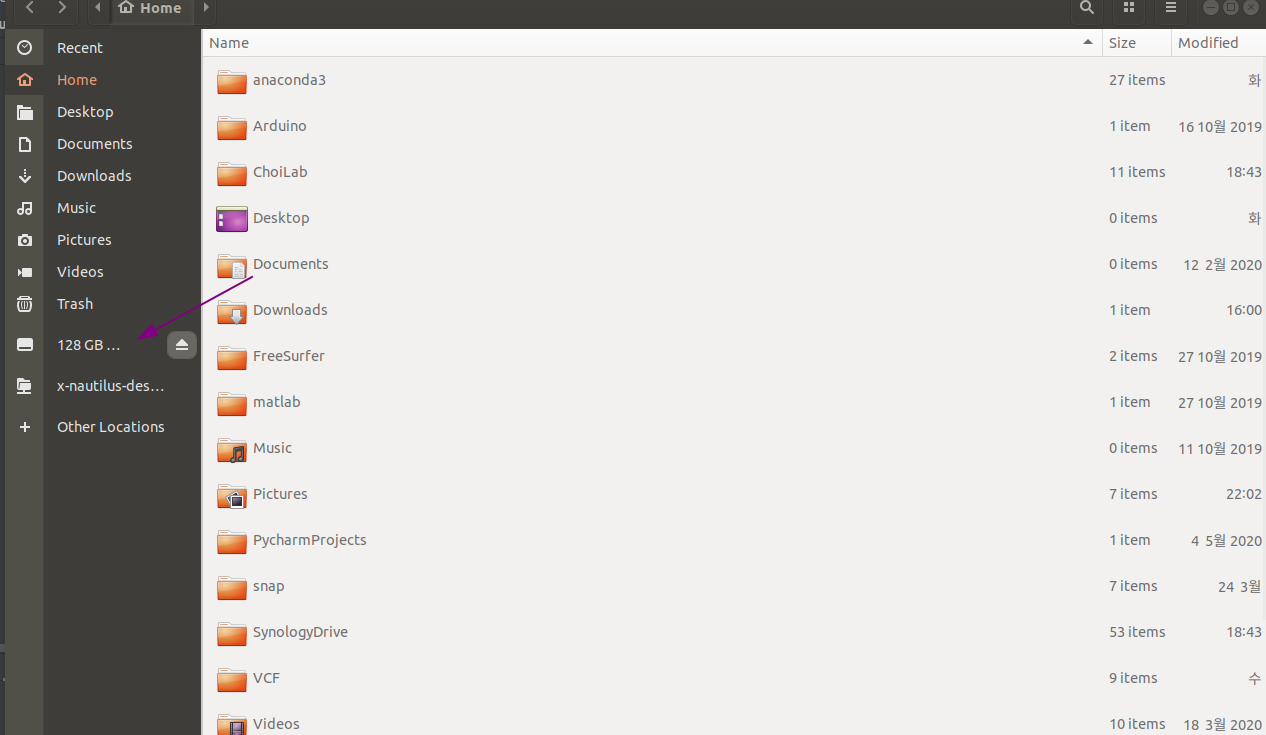
- 하지만 리눅스의 목적에 맞게 결국 콘솔을 더 자주 사용하게 된다. 콘솔은 Ctrl+Alt+t로 열 수 있다.
콘솔 기본 커멘드
- 기본으로는 bash라는 쉘이 돌아간다. 이 이외에 zsh, csh, tcsh 등 다양한 것들이 있고 다들 bash를 안 쓰고 다른 shell을 쓰는 것 같은데 이유는 아직 모르겠다. 더 좋겠지 뭐. 아직은 불편함을 못느껴서 그대로 사용중이다.
- 도움말 보기 : man 모르는커맨드 를 입력하거나 모르는커맨드 -h 혹은 모르는커맨드 --help 를 입력하면 대체로 알려준다.
- cd : change directory : 뒤에 경로를 입력해서 현재 위치를 바꾼다
- ls : list files : 현재 위치에서의 파일들을 출력한다. 주로 -alF 옵션을 함께사용하며 대체로 ll 이라는 alias로 등록이 되어있다.
- mv, rm, cp : move, remove, copy
- | 표기 : 가끔 출력된 내용이 너무 많은 경우 콘솔 창 위로 쭉 올라가 버리는 경우가 있다. 이를 천천히 볼 수 있도록 할 때 출력결과를 다른 프로그램에 feed 해줄 수 있는데 이때 이 | 표기를 사용하며 pipe 라고 한다.
- | more 혹은 | less : 출력결과를 보기 편하게 해준다.
- | grep 검색어 : 출력결과에서 검색어가 있는 행만 보여준다.
- 예) ll | grep *.txt : 현재 위치에서 파일리스트를 출력하고 이중 .txt 확장자를 가진 애들만 출력.
- > 표기 : 출력된 내용을 뒤의 파일에 저장(overwrite) : ls > result.txt
- >> 표기 : 출력된 내용을 뒤의 파일에 저장(append) : ls >> result.txt
- < 표기 : 뒤의 파일의 내용을 불러와 커맨드 실행 : sort < filelist.txt
- 프로세스
- ps : 현재 프로세스를 확인
- kill : 프로세스를 강제 종료. -9 옵션을 주면 무조건 종료된다고 함.
- fg 숫자 : 숫자로 표시된 프로세스를 foreground로.
- Ctrl+z : 프로세스 일시중지
- bg : 프로세스를 backgroud로.
- 커맨드 마지막에 &를 붙이기 : 해당 커맨드를 background로 실행
- jobs : background에서 돌아가는 프로세스를 확인
자주는 안썼지만 써본 콘솔 커멘드
- lsblk : list block devices : 연결된 저장장치 확인이 가능
- df : disk space usage report
- mount : lsblk를 사용해서 연결된 저장장치를 확인하고 (예: /sdb1) 이를 원하는 경로에 mount 가능
- sudo mkdir /media/사용자명/mydrive
- sudo mount /dev/sdb1 /media/사용자명/mydrive
- lsof : list open files : 출력량이 상당히 많음....
- lsmod : list modules
- rmmod : remove module
/etc 내부의 파일/폴더
- apt : 패키지 관리 프로그램
- cron : 특정 시간에 특정 작업을 할 수 있도록 해주는 프로그램이라고 함. 예약된 작업?
- ca-certificate : 각종 인증서(?)
- fstab : 자동 mounting 프로그램
- fonts
- wpa_supplicant : wifi 정보 관련
'취미 > Programming' 카테고리의 다른 글
| Ubuntu TensorFlow(2.6) GPU 설치 (0) | 2021.09.06 |
|---|---|
| Matlab과 Python에서의 image 좌표축 한번에 정리! (0) | 2021.06.16 |
| [Vim] Linux 상에서의 Not an editor command: ^M 문제 (0) | 2021.03.24 |
| Python(anaconda) Vim intagration (2) | 2020.10.28 |
| Multi Layer Perceptron (MLP) (1) | 2020.05.06 |
현재 한 컴퓨터에서 Ubuntu와 Windows를 같이 사용중이다.
지금까지 3번정도 Ubuntu 사용을 해보려고 시도했었지만 적은 사용량과 한글 문서등의 호환성 이슈 때문에 사용을 포기했었으나 지금은 그래도 꾸준히 사용을 하고 있다.
이전 글에도 올렸지만 주력 text editor로 vim을 사용한지가 꽤 되었는데 아직도 Ubuntu에서는 최신 vimrc 파일을 설치해두지 않았더라.
그래서 그대로 _vimrc 파일을 긁어다가 Ubuntu에 .vimrc로 넣어주었는데 이게 무슨 일! vim을 로딩할때 넘쳐나는 에러의 향연을 볼 수 있다.
한 두개야 vim 버전 문제겠지하고 넘겼을 수 있었겠지만 수십개가 주르륵 나오는 것으로 바로 알아차렸다.
아, 이거 100% 인코딩이나 Line ending 문제다.

아니나다를까 Unix-based 시스템과 DOS-based 시스템의 Line ending이 다르단다.
분명 어딘가에서 읽었을 것 같은데 당시에는 Unix-based 시스템을 쓸 일이 없다고 생각했고 앵간한 상용 프로그램들은 이런 문제를 알아서 해결해주기에 'Line ending이란게 있다더라~' 하고 넘어간듯 하다.
다행히 구글에서 비슷한 케이스를 바로 찾을 수 있었는데 별로 반가운 대접을 받지는 못하는 것 같다.
(그도 그럴게 issue에 bug report 처럼 올렸으니... )
github.com/vim/vim/issues/6156
E492: Not an editor command: ^M on Linux subsystem · Issue #6156 · vim/vim
I installed Vim on Ubuntu via Linux Subsystem on Windows 10, so I can use it for work. I changed the home directory to the Windows user directory and symlinked the Ubuntu home to it. I use VimPlug ...
github.com
Solution
vim wiki에 가보니 친절한 설명이 되어있다.
vim.fandom.com/wiki/File_format
File format
Vim recognizes three file formats (unix, dos, mac) that determine what line ending characters (line terminators) are removed from each line when a file is read, or are added to each line when a file is written. A file format problem can display ^M characte
vim.fandom.com
결국 모든 문제의 근원은 엔터를 칠 때 CR(Carriage Return)과 LF(Line Feed)(New Line이라고 하기도 함)를 자동으로 입력해주는 DOS에서 가져온 텍스트 파일을 LF만 사용해서 새 줄을 표기하는 Unix 시스템이 읽고 "CR이 뭐임?" 하는 상황 때문에 문제가 발생하는 것이다.
참고로 CR은 0x0D 이며 이는 Ctrl-M과 대응된다.
CR과 LF의 유래에 대해서는 아래 글에 자세히 나와있다.
일반적인 text 파일의 경우 해결 방법은 크게 1)CR을 지워주거나 2)CR을 무시하게 하거나 둘 중 하나이지만, vim 시작후 가장 먼저 읽어들이기 시작하는 vimrc 파일의 경우는 1)CR을 지운 버전을 사용하는 방법밖에 없는 것 같다.
(CR을 무시하게 하는 방법이 있다면 꼭 알려주세요)
1. dos2unix 유틸리티 설치 후 CR을 지워주기.
sudo apt-get install dos2unix
dos2unix ~/.vimrc
2. vim의 substitute 기능을 사용해 CR을 지워주기.
^M 을 vim 커멘드에 입력하기 위해서는 Ctrl-v를 누른후 Ctrl-m을 눌러야 한다.
:%s/^M//g
'취미 > Programming' 카테고리의 다른 글
| Matlab과 Python에서의 image 좌표축 한번에 정리! (0) | 2021.06.16 |
|---|---|
| Ubuntu setup (Linux setup) (0) | 2021.06.11 |
| Python(anaconda) Vim intagration (2) | 2020.10.28 |
| Multi Layer Perceptron (MLP) (1) | 2020.05.06 |
| [GitHub] 3. GUI Git: GitHub Desktop, Sourcetree, GitKraken (0) | 2019.11.13 |
서론
온갖 것들에 관심을 주는 성격 때문인지 한 언어의 실력을 진득히 늘리기 보다는 온갖 언어를 조금씩 하게 된 것 같다.
그 덕에 디자인 때문에 왠지 좋아하는 Visual Studio 부터 기억도 안나는 Eclipse, 의외로 자주 열게되는 sublime text까지 다양한 IDE(Integrated Development Environment)를 사용해봤다.
다행히 MATALB과 python은 연구에서 쓰느라 자기 손 처럼 익숙해지기도 했는데 이 python이 정말 IDE가 골치아프다.
인터프리터 기반 언어는 MATLAB이 처음이었는데 깔끔한 상업용 IDE에 익숙해지다 보니 python을 배울 때 정말 애를 먹었다. 메모장으로 시작해 Spyder로 잠깐 넘어갔다가 PyCharm을 발견하고 지금까지 쓰고 있다.
Interpreter Environment 설정부터 git관리까지 완벽하게 해주고 중간부터는 numpy 지원을 해서 깔끔한 gui로 거의 MATLAB급의 환경을 제공해주더라. 게다가 학교에 있는 경우 professional version이 무료! 파이썬 시작한다는 사람들에게 엄청 홍보하고 다녔다.
그런데, 사실 프로그래밍 할 때 IDE의 얼마나 많은 기능들을 쓰는가 싶다.리소스를 고려할만큼 무거운 것들을 돌리지 않으니 리소스 모니터도 필요 없고. 프로젝트라고 불리울만큼 여러 소스코드가 뒤섞여있지 않고, 심지어 버전관리도 따로 프로그램을 돌리기에 사용하지 않는다.
내가 python을 쓸 때 메모장을 쓰지 못하는 이유 를 적어보니 아래와 같이 나오더라.
- 간단한 단축키로 line by line으로 프로그램 돌리기
- 자동완성
- syntax highlighting
- 파일 탐색기 integration
부끄럽게도 정말 이게 다 더라.
compiler 를 사용하는 언어라면 그래도 디버깅을 하며 IDE를 쓸 텐데 python을 쓸 때는 정말 살짝 좋은 메모장 이상의 기능은 쓰고 있지 않았다.
그러던 와중 찐 코딩덕후들이 사용한다는 vim이 떠올랐다.
리눅스 환경에서 코딩을 할 때 가끔 쓰고 i를 누르면 편집, :w를 누르면 저장, :q를 누르면 나가기가 된다는 정도만 알고 있었는데 이게 그렇게 배워두면 뒤로 못 돌아간다더라.

키보드에 난잡하게 있는 커멘드 때문에 두번 포기하고 3번째에야 불편하지는 않을 수준으로 쓰게 되었다만 역시 쓸 일이 없으니 계속 잊을 것 같았다.
그러던 어느날 친구 컴퓨터에서 코딩을 도와주다가 위로 올라가기 위해서 k를 연타하는 자신을 본 순간 깨달았다.
아! 이제 Vim으로 코딩을 해도 되겠다!
다행히 그 명성에 걸맞는 확장성 때문에 + 인터프리터 언어의 특성 때문에 python과 vim은 상성이 아주 잘 맞는다.
단지 윈도우에서 셋업을 하는데 조금 어려울 뿐이다.
가장 좋은 점은 위에서 언급한 execute selected line(s), autocompletion, syntax highlighting, file explorer integration의 모든 기능들을 vim plugin들로 구현할 수 있다.
기록을 남겨둘 겸 몇가지 초기 세팅을 적어두려고 한다.
VIM 설치
python을 쓰는데 anaconda를 쓰지 않을 인간은 없다. 에이 설마. 적어도 연구자들은 anaconda가 안깔려 있으면 거의 100% 이제 막 파이썬을 시작한 것이더라. 그래서 anaconda로 python이 설치되어있다고 가정하고 글을 쓴다.
일단 Path 안에 다른 python이 있지 않은지 확인을 해서 한 컴퓨터 안에 여러개의 python이 돌아다니는 일을 먼저 해결하고 시작해야한다.
기본 옵션으로 anaconda를 설치했으면 cmd 창에서는 python이 실행이 안된다. 요즘은 python이 없는 상태로 커멘드를 입력하면 Microsoft store로 연결해주던데 귀찮게 시리.
Python을 실행하려면 anaconda prompt를 켜서 그 안에서 실행을 해야한다. 그러면 해당 가상 환경에 걸맞는 파이썬이 로드될 것이다.
때문에 vim을 실핼할 때도 cmd로 실행하는 것이 아니라 anaconda prompt 내에서 실행을 해야한다.
지나가다가 보기로는 가상 환경 지원도 해주는 것 같던데 일단 오늘은 기본 (base)에서 돌아가게 하는 것을 전제로 한다.
Window 버전 설치 링크는 다음과 같다.
github.com/vim/vim-win32-installer/releases
Releases · vim/vim-win32-installer
Vim Win32 Installer. Contribute to vim/vim-win32-installer development by creating an account on GitHub.
github.com
그리고 아주 중요한 것.
VIM을 설치할 때는 꼭! anaconda의 32-bit / 64-bit 버전과 맞는 것을 설치해야 한다.
이것 때문에 1시간을 버렸다. 만약 이것을 지키지 않으면 나중에 아래의 메시지를 보게 될 것이다.
E370: Could not load library python38.dll
E370: python38.dll 라이브러리를 로드할 수 없습니다.
E263: Sorry, this command is disabled, the Python library could not be loaded
E263: 미안합니다, 이 명령은 사용할 수 없습니다, 파이썬 라이브러리를 로딩할 수 없습니다.설치할 때 다른 옵션은 그대로 두고 설치해도 좋다. 그냥 다음 다음 다음 클릭.
Vundle설치 이제는 Vundle 보다는 Vim-Plug를 더 많이 쓰는 것 같다.
vim의 pip과 같은 Plugin 설치에 있어서 착한 기능을 하는 친구가 vundle이다.
이것도 윈도우에서 설치시 에러사항이 있는데 instruction을 따라서 3번이나 설치해봐도 항상 똑같이 제대로 설치가 안되더라. 내가 3번 다 메뉴얼을 잘못 읽었을 가능성도 있다. 어느 누가 풀리퀘를 걸지 않았으려나.
여튼, 내가 한 방법은 다음과 같다.
먼저 git for windows를 설치한다.
anaconda prompt에서 git 입력시 반응이 나타나면 넘어가도 좋다.
설치 링크는 아래와 같다.
Git - Downloading Package
Downloading Git Now What? Now that you have downloaded Git, it's time to start using it.
git-scm.com
공식 페이지 설명을 보면 curl도 필요하다고 하는데 win10은 같이 딸려나온다고 하니 신경쓰지 않아도 될 듯하다.
리눅스 유저라면 헷갈릴수도 있는게 window 용 vim은 .vimrc 대신 _vimrc, ~/.vim 대신 ~/vimfiles 를 사용한다.
그리고 공식 설명에서는 아래의 코드를 그대로 쓰면 된다고 하지만 왜인지 내 cmd는 ~를 홈으로 인식하지 않는다.
powershell을 쓴다면 아래의 코드를 그대로 쓰고
git clone https://github.com/VundleVim/Vundle.vim.git ~/vimfiles/bundle/Vundle.vim검은창이 익숙하다면 유저명을 적절히 바꿔서 넣고 아래를 쓰자.
git clone https://github.com/VundleVim/Vundle.vim.git C:/Users/유저명/vimfiles/bundle/Vundle.vim마지막으로 vim을 실행한 후 아래 커멘드를 입력해주면 된다.
:PluginInstall
Vim-Plug 설치
이 글을 작성하는 와중에 알게 되었는데 Vundle 보다는 Vim-Plug가 더 깔끔하고 gui 같은 그래픽을 만들어 놓은 것이 기특하다. Plug를 쓰는 것이 더 좋을 듯 하다.
설치는 정말 간단하다. powershell에서 아래 코드를 실행하자.
iwr -useb https://raw.githubusercontent.com/junegunn/vim-plug/master/plug.vim |`
ni $HOME/vimfiles/autoload/plug.vim -Force
(현명하게도) 주인장을 믿지 못한다면 공식 페이지 설치법을 체크하자
junegunn/vim-plug
:hibiscus: Minimalist Vim Plugin Manager. Contribute to junegunn/vim-plug development by creating an account on GitHub.
github.com
ctags 설치 (옵션)
다른 프로그래머들의 _vimrc 파일을 구경하다가 Vista 라는 Plugin을 찾았는데 이게 상당히 쓸만한 친구인것 같다.
약간 고급 IDE의 프로젝트 브라우져 같은 것인데 어떤 함수가 어디에서 정의되어 있는지 현재 정의한 변수는 무엇인지 등을 알려준다.
이정도면 그냥 Visual Studio나 PyCharm을 하나 만드는 것 같은데..???
설치방법은 아래와 같다.
이 링크에서 최신 release에 들어간 뒤, 설치한 빔 버전에 맞는 (32/64) release 파일을 받는다.
github.com/universal-ctags/ctags-win32/releases
Releases · universal-ctags/ctags-win32
Universal Ctags Win32 daily builds. Contribute to universal-ctags/ctags-win32 development by creating an account on GitHub.
github.com
이후 압축을 풀고 시스템 경로의 Path 안에 포함되어 있는 아무 폴더에 .exe 파일 두 개를 넣어주면 된다.
나는 vim 커멘드를 쓰기에 그냥 vim.exe 파일이 있는 C:\Program Files\Vim\vim82 안에 넣어두었다.
기타 Plugin 설치
설치할 플러그인은 아래와 같다.
- Vim-sensible : 설명을 읽어봐도 모르겠으나 다들 설치하더라(?)
- vim-vuftabline : 버퍼에 넣은 텍스트를 탭으로 보이게 해준다
- nerdtree : 파일 탐색기
- vim-nerdtree-tabs
- vim-gitgutter : git 연동
- nerdtree-git-plugin
- Jedi-vim : 자동완성
- supertab : 자동완성시 tab 사용 가능
- ale : 에러 체크
- vista : ctags를 사용하는 프로젝트 익스플로러st 한 기능
- lightline : 하단 상태바
- onedark : 어두운 colorscheme
- Vim-monokai-tasty : 모노카이가 아니면 코딩을 못하는 병에 걸렸다
이는 _vimrc(.vimrc) 변경후 아래의 커멘드를 실행해주면 된다.
:PlugInstallVista.vim 에러 해결
Vista.vim을 까는 중에 아래의 에러가 발생하였다.
17 줄:
E696: List에 콤마 누락: ??])
E116: 함수 get(g:, 'vista_fold_toggle_icons', ['??, '??])(으)로 잘못된 인자가이 역시 반복되는 재설치, 플러그인 정리로 한참을 시간을 보낸 뒤에야 원인을 알게 되었다.
.vim 파일을 뜯어보니 아이콘을 사용하기 위해서 ▼▶ 기호를 쓰는데 아무래도 망할 인코딩 문제인듯 했다.
_vimrc 파일에 앞에 인코딩 부분을 설정해주니 문제 없이 작동한다.
" sane text files
set fileformat=unix
set encoding=utf-8
set fileencoding=utf-8첨부한 _vimrc에는 반영이 되어 있으니 그대로 실행하면 된다.
Python 연결
사실 여기까지 실행하면 아래 기능들이 끝난 것이다.
- 간단한 단축키로 line by line으로 프로그램 돌리기
- 자동완성
- syntax highlighting
- 파일 탐색기 integration
안타깝게도 아직 line by line으로 python을 돌리는 것을 찾아내지 못했다.
일단 vim 내부에서 Anaconda Python을 연동시키기 위해서는 무엇보다 vim 자체를 anaconda prompt에서 실행하는 것이 제일 먼저고 _vimrc 파일안에 아래의 라인이 필요하다.
set pythonthreehome=~\anaconda3\
set pythonthreedll=~\anaconda3\python37.dll아무래도 저게 없으면 python을 쓰는 jedi plugin의 기능이 먹통이 된다.
Anaconda로 python을 설치하면 경로를 못찾아서 그런지 저런 오류가 발생하는 듯 하다.
Anaconda의 경로가 다른 경우 거기에 맞춰서 스크립트를 적절히 수정하기 바란다.
또한 이것 역시 설치한 python의 아키텍쳐 버전과(32/64) vim의 버전이 맞아야 실행이 된다는 점을 기억하자.
vim에서 python을 사용하는 방식은 크게 두 가지 이다.
1. !로 콘솔 커멘드에서 python을 실행시키기
:1,5w !python위의 예시는 첫 줄 부터 5줄까지 쓰고, (원래는 파일에 쓰는 것이겠지만 이번은 python에 통쨰로 코드를 넘겨주는 것이다.) 이를 외부에서 python를 사용해 실행시키는 방식이다.
권장되는 방법이며 한번 실행이 된 스크립트는 실행 후 결과를 표시한 뒤, 종료된다. 따라서 데이터가 남지 않는다.
2. py3 커멘드로 vim 내부에서 python을 실행시키기
:py3 print("hello world")위의 예시는 즉각 뒤에 오는 string을 python으로 실행시킨다.
:py3 로 실행하는 스크립트는 vim과 연동된 스크립트라 vim에서 데이터 입출력이 가능하며, vim이 종료되지 않는 이상 이전 실행 결과과 유지도니다.
하지만 이 커멘드는 아직 파일내 영역을 지정해서 실행하는 방법을 찾지 못했다.
doc string을 읽어보면 범위 옵션이 있긴 한데 열심히 커뮤니티를 찾아봐도 알아내기 힘들었다.
방법을 알아낸다면 블로그지기에게 알려주시고 블로그지기가 먼저 알아낸다면 수정해서 올리겠다.
Code snippet execution (Python)
블로그지기는 인터프리터 계열 언어를 사용할 때 창을 두 개 띄워두고 한 창에서 한 줄 한 줄 코드를 실행시키면서 테스트를 한 뒤 이를 다른 창에 옮겨 이를 나중에 활용한다.
예를 들어 1)데이터 로드 -> 2)전처리 -> 3)분석 구조의 스크립트를 짤 때 매번 전체 스크립트를 실행시키지 않고 1)을 끝내두었으면 1) 까지를 실행시켜둔 콘솔에서 2)를 중간중간에 콘솔에 넘겨 실행시켜본다.
컴파일러 계열 언어라면 전체를 돌리고 그 안에서 breakpoint를 넣어가며 디버깅을 해야겠다만 인터프리터라면 왜 굳이.. 그런데 이게 일반적인 방법이 아닌가보다. 코딩을 혼자 배우면 이렇게 된다
때문에 이미 짜둔 스크립트의 일부를 콘솔에 옮겨서 실행해야할 경우가 빈번히 발생하는데, 고급 IDE에서는 현재 줄 실행, 선택 영역 실행 등의 기능이 있어서 단축키를 등록해두고 자주 사용해왔다.
그런데 이게 vim에 없다!
거의 5시간은 찾았는데 플러그인은 커녕 누가 시도한 것을 찾지도 못했다!
세상에.. 그나마 비슷한 것은 https://vim.fandom.com/wiki/Evaluate_current_line_using_Python 이 팁인데 이것은 한 줄만 실행이 가능한 미완성 상태로 남아있다.
심지어 이번에 처음 알았는데 python의 eval 함수는 'a=3' 등의 대입문을 처리하지 못한다더라.
그래서 어찌저찌 하나를 만들었다. vim 을 사용한지 누적 5시간도 안되는 뉴비가 만든 것임을 인지해주기를 바란다.
다음의 코드를 _vimrc에 넣고 vim에서 :Eval을 실행하면 된다.
"Python execute selected line script
python3 << EOL
import vim
def ExecuteSelectedLine(l1, l2):
for i in range(l1-1,l2):
print(">>" + vim.current.buffer[i])
exec(vim.current.buffer[i],globals())
EOL
command! -range Eval <line1>,<line2> python3 ExecuteSelectedLine(<line1>, <line2>)- :Eval : 현재 줄 실행
- :1,3Eval : 1~3째 줄 실행
- '<,'> : visual 모드로 선택된 영역 실행
다음은 _vimrc 파일의 예시이다.
" vim runtime config file
" Written by Knowblesse 2020
" Adapted from miguelgrinberg/.vimrc
" sane text files
set fileformat=unix
set encoding=utf-8
set fileencoding=utf-8
call plug#begin()
Plug 'tpope/vim-sensible'
"buffer lists instead of tab
Plug 'ap/vim-buftabline'
"NERD
Plug 'preservim/nerdtree'
Plug 'jistr/vim-nerdtree-tabs'
"Git
Plug 'airblade/vim-gitgutter'
Plug 'Xuyuanp/nerdtree-git-plugin'
"Coding
Plug 'davidhalter/jedi-vim'
Plug 'ervandew/supertab'
Plug 'dense-analysis/ale'
Plug 'liuchengxu/vista.vim'
Plug 'itchyny/lightline.vim'
"Color theme
Plug 'flazz/vim-colorschemes'
Plug 'joshdick/onedark.vim'
call plug#end()
set tabstop=4
set shiftwidth=4
set softtabstop=4
set colorcolumn=100
set expandtab
"HighLight SEARCH result
set hlsearch
set pythonthreehome=~\Anaconda3\
set pythonthreedll=~\Anaconda3\python37.dll
autocmd FileType python setlocal completeopt-=preview
set guifont=Bitstream\ Vera\ Sans\ Mono:h14
" indent/unindent with tab/shift-tab
nmap <Tab> >>
nmap <S-tab> <<
" color scheme
syntax on
colorscheme Monokai
filetype on
filetype plugin indent on
" lightline
set noshowmode
let g:lightline = { 'colorscheme': 'onedark' }
let g:nerdtree_open = 0
map <leader>t :call NERDTreeToggle()<CR>
function NERDTreeToggle()
NERDTreeTabsToggle
if g:nerdtree_open == 1
let g:nerdtree_open = 0
else
let g:nerdtree_open = 1
wincmd p
endif
endfunction
function! StartUp()
if 0 == argc()
NERDTree
end
endfunction
autocmd VimEnter * call StartUp()
"Python execute selected line script
python3 << EOL
import vim
def ExecuteSelectedLine(l1, l2):
for i in range(l1-1,l2):
print(">>" + vim.current.buffer[i])
exec(vim.current.buffer[i],globals())
EOL
command! -range Eval <line1>,<line2> python3 ExecuteSelectedLine(<line1>, <line2>)
정리가 잘 안된 감이 있지만 언젠가 더 vim에 익숙해지면 깔끔하게 정리하겠지.
마지막으로 아래 커맨드를 실행을 잊지 않는다
:PlugInstall
마치며
피곤하다.
완성된 IDE에 벌써 정이가는데 이렇게 배우는데 시간을 들인만큼 생산성도 같이 올라가면 좋을 듯 하다.
깔끔한 책 구성으로 vim을 쉽게 배우는데 도움을 주신 김선영 선생님께 감사의 말씀을 멀리서 전하고 싶다.
정말 추천하는 책이다.
www.aladin.co.kr/shop/wproduct.aspx?ItemId=11228613
손에 잡히는 Vim
Vim의 필수 기능들을 친절한 그림과 함께 차근차근 설명하여, ‘배우기 어려운 에디터’라는 고정관념을 깨뜨린다. 리눅스를 공부하는 학생이나 터미널 창에서 작업하는 서버 관리자, 키보드에
www.aladin.co.kr
'취미 > Programming' 카테고리의 다른 글
| Ubuntu setup (Linux setup) (0) | 2021.06.11 |
|---|---|
| [Vim] Linux 상에서의 Not an editor command: ^M 문제 (0) | 2021.03.24 |
| Multi Layer Perceptron (MLP) (1) | 2020.05.06 |
| [GitHub] 3. GUI Git: GitHub Desktop, Sourcetree, GitKraken (0) | 2019.11.13 |
| [GitHub] 2. git과 GitHub의 관계 (0) | 2019.11.12 |
처음 Perceptron의 개념을 접한지 벌써 6년이 지났다.
당시 Single Layer Perceptron (SLP)만 배웠었는데 신경망의 작동원리를 표방한 구조가 마음에 들어 다른 서적까지 뒤져가며 개념을 이해하려고 애썼다.
선형대수도 제대로 알지 못했는데 구조가 단순해서 그런지 수학적으로 완벽하게 개념을 이해할 수 있었다.
과제로 나온 문제 중 하나가 '왜 SLP는 XOR 문제를 풀지 못하는지 설명하라' 였는데 이에 대해서 완벽한 답을 내놓았을 때의 짜릿함이란...
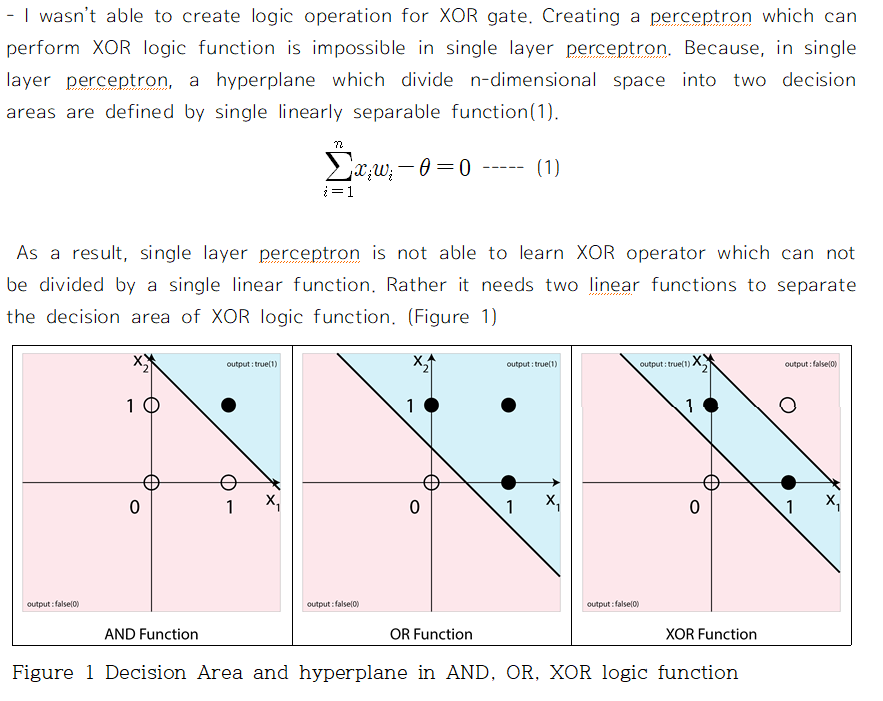
SLP는 그 이후로도 다른 수업이나 특강에서 접할 기회가 많아서 익숙해졌지만 , 아직까지 Multi Layer Perceptron (MLP)를 완벽하게 이해하지 못했다. 수식을 외워서 어찌저찌 코드를 짤 수는 있었지만 왜 저런 수식이 나오는지 개념적으로 설명을 하지 못했다.
지난 코드들을 정리하던 중 짜다 포기한 MLP 코드가 있길래 지금이라면 이해할 수 있지 않을까 하고 도전한 결과, 드디어 오랫동안 끝내지 못한 과제를 해결하게 되었다.
이해한 개념을 잊지 않도록 SLP부터 정리하고 기록하려고 한다.
Single Layer Perceptron
Perceptron 구성에 필요한 것
- input node의 수
- output node의 수
- 초기 weight 값
- learning rate
- epoch 수
먼저 network를 구성하기 위해서 필요한 것은 input node와 output node의 숫자다.
input node의 수 : j
output node의 수 : k
일반적으로 "한 개"의 perceptron은 여러 개의 input을 받아서 하나의 output을 출력하는 대상을 말하기에 output node가 k개 있는 위의 예에서는 k개의 perceptron이 하나로 합쳐져 있는 것이라고 생각해야 한다.

또 필요한 것은 사실상 학습이 일어나는 변수인 weight의 초기값이다.
위와 같이 모든 node 들이 서로 연결된 fully-connect 조건인 경우 input node의 수 x output node의 수 (j x k) 만큼 weight 값이 필요하다.
Output node에서는 이후 input node의 값들을 각각의 weight로 곱해주고 threshold를 넘냐 안넘냐로 output을 바꾸는데 이게 꽤 귀찮다.
왜냐하면 이 threshold를 잘못 정하면 학습이 전혀! 일어나지 않기 때문이다.
그래서 사용하는 방법이 input node가 비록 j개만큼 있지만 항상 1 값을 내놓는 가상의 node를 만들고 weight의 수를 (j x k)가 아닌 (j+1 x k) 로 설정하는 것이다.
이러면 모든 output node의 threshold를 0으로 설정해도 이 가상의 node를 통해 threshold 값이 조정된다.
이러한 가상의 node를 bias 라고 한다.

이렇게 하면 나중에 weight update를 할 때 weight 값이 바뀌면서 각각의 node의 threshold가 바뀌게 되고, 각 node 별로 최적의 threshold가 구해질 것이다.
weight matrix : W => (j +1 x k)
초기 weight 값을 구하는 것에는 다양한 방법이 있으나 편의상 -1과 1 사이의 무작위 값으로 쓰도록 하자.
마지막으로 매번 학습마다 weight 값을 얼마만큼 바꿀지에 대한 learning rate (보통 0.1 정도면 충분) 와 전체 training sample을 몇번 돌려가며 학습을 시킬지에 대한 epoch ( 일단 100정도) 이 필요하다.
import numpy as np
# Constants
num_input_node = 4
num_output_node = 3
learning_rate = 0.1
num_epoch = 100
# Variables
weights = np.random.rand(num_input_node + 1, num_output_node) * 2 -1
# rand 함수는 0~1 사이 값을 주기에 x2-1을 하면 -1과 1 사이의 값이 나온다.Feed Forward 계산
j+1개의 값들을 각각의 weight들과 곱한 뒤, 합하는 작업을 총 perceptron의 수인 k번 해야한다.
물론 Method 1처럼 for 문을 두 번 사용하면 해결이 되겠지만 Method 2처럼 코드 한줄로 모든 연산을 끝낼 수 있다.
바로 선형대수를 이용하는 것이다.
# Method 1
for perceptron in range(k):
for node in range(j+1):
output_node[perceptron] += weight[node, perceptron] * input_node[node]
# Method 2
output_node = np.dot(weight.T, input_node)
대학원 인공지능개론 수업에서는 교수님이 학생들이 전부 선형대수를 완벽히 알고있다고 가정하고 설명을 하시던데 물리/정보계 이과가 아니어서 그런지 나는 고등학교때 행렬 연산 지식이 전부다.
이 수업을 따라가려고 선형대수로 유명하다는 Strang 교수님의 선형대수 책 스터디도 진행을 했는데 정작 머릿속에 남아있는 개념은 딱 두 가지이다.
행렬의 곱, dot product와 dot product 에서의 차원 계산
1. The dot product (행렬의 곱)
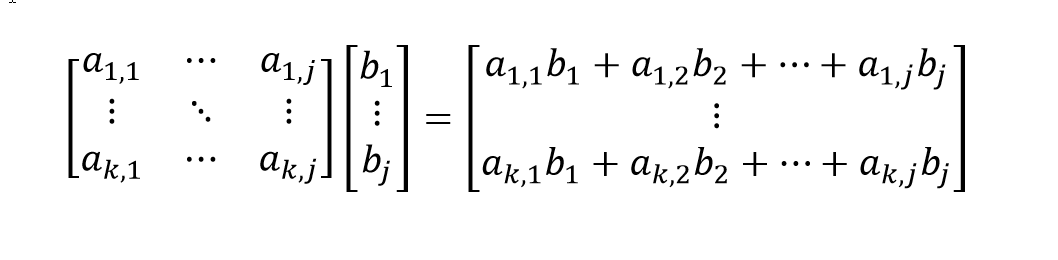
k x j 형태의 matrix와 j x 1 형태의 matrix (혹은 columnar vector) 의 Dot product는 위와 같이 계산된다.
복잡해보이지만 좌측 matrix의 한 행의 원소들(총 j개)를 각각 같은 위치에 있는 우측 matrix의 열의 원소들(총 j개)로 곱해준 뒤 이를 전부 합해주면 한 행의 element가 완성이 된다.
어짜피 하는 연산은 for 문 2개를 돌리는 것과 같지만, 이렇게 각각의 원소들을 다른 matrix의 대응하는 원소와 곱한뒤 이를 합하는 연산이 Perceptron 외에도 정말 자주 등장하기에 수학에서 이러한 연산을 dot product라고 따로 정의한 것 같다.
물리에서 벡터 연산이나 간단한 선형 방정식에서도 자주 본 적이 있다.
2. The dimension of the dot product
위에 언급한 부분을 잘 보면 두 matrix의 dot product를 구할 때 중요한 조건이 있다.
"좌측 matrix의 한 행의 원소들(총 j개)를 각각 같은 위치에 있는 우측 matrix의 열의 원소들(총 j개)로 곱해준 뒤 이를 전부 합해주면 한 행의 element가 완성이 된다."
바로 좌측 matrix의 열의 수와 우측 matrix의 행의 수가 일치해야 연산이 가능하다는 것이다.
또한 연달아 dot product를 계산하면 최종 결과는 최좌단 matrix의 행의 수 x 최우단 matrix의 열의 수 가 된다.
예를들어, matrix A, B, C가 각각 axb, bxc, cxd 의 차원을 가지고 이들은 전부 곱하면, 최종결과는 a x d가 된다.
이 개념이 아주 중요하다.
끽해야 2-3개의 행과 열로 된 matrix를 다루는 손으로 푸는 문제는 바로 어떻게 연산을 해야할지 보이는데, 수십, 수백개의 행과 열로된 matrix를 컴퓨터로 연산을 할 때는 matrix의 구조가 보이지 않아서 차원이 맞지 않는 오류가 나기 쉽다.
그래서 곱해야할 것들을 정하고, 원하는 결과의 차원을 정한뒤, matrix 자체는 보지 않고 matrix의 dimesion만 보면서 코딩을 해나간다.
다시 SLP로 돌아가서, 현재 weight은 (j +1 x k)로 되어있고, input node의 수는 j+1.
원하는 연산을 위해서는 weight matrix의 행과 열을 바꾸고 bias를 포함한 input node와 곱해주면 된다.
참고로 이렇게 행과 열을 바꿔주는 행위를 transpose 라고 하고 위에 작은 T 첨자를 붙인다.

처음 배울때 선형대수만큼 짜증나는 것은 없다!
덧셈과 곱셈만 있음에도 당장 위에 수식만 봐도 머리가 돌아버릴 것 같다.
그런데 저런 모든 과정을 ∑ 기호를 쓰지 않고 아래와 같이 단순한 기호로 표시할 수 있다는 것은 정말 큰 장점이다.

처음에만 위에 기나긴 수식을 하나 하나 따라가면서 이해하고, 그 이후로는 각 matrix의 차원만 봐도(얘가 j x k 인지 k x j 인지) 전혀 문제가 없으니 걱정 마시라!
우리가 해야할 부분은 dot product를 언제 써야하는지 아는 것과, dot product를 낼 두 matrix의 차원을 맞춰주는 것 뿐이다.
import numpy as np
# Constants
num_input_node = 4
num_output_node = 3
learning_rate = 0.1
num_epoch = 100
# Variables
weights = np.random.rand(num_input_node + 1, num_output_node) * 2 -1
# rand 함수는 0~1 사이 값을 주기에 x2-1을 하면 -1과 1 사이의 값이 나온다.
##############################여기부터##############################################
# Feed Forward
input_node = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)Backpropagation 계산
다음 단계는 총 k개의 perceptron마다 나온 a 값을 실제로 나와야 하는 값이랑 비교하는 것이다.
desired output의 d를 따서 d라고 부르겠다.
Error = desired output(d) - actual output(a)
a 값이 k x 1 의 형태로 나올 것이기에 desired output도 똑같이 모든 perceptron, 혹은 output node의 desired output 값을 column vector 화 해서 서로 빼주면 k x 1 의 형태로 error를 구할 수 있다.
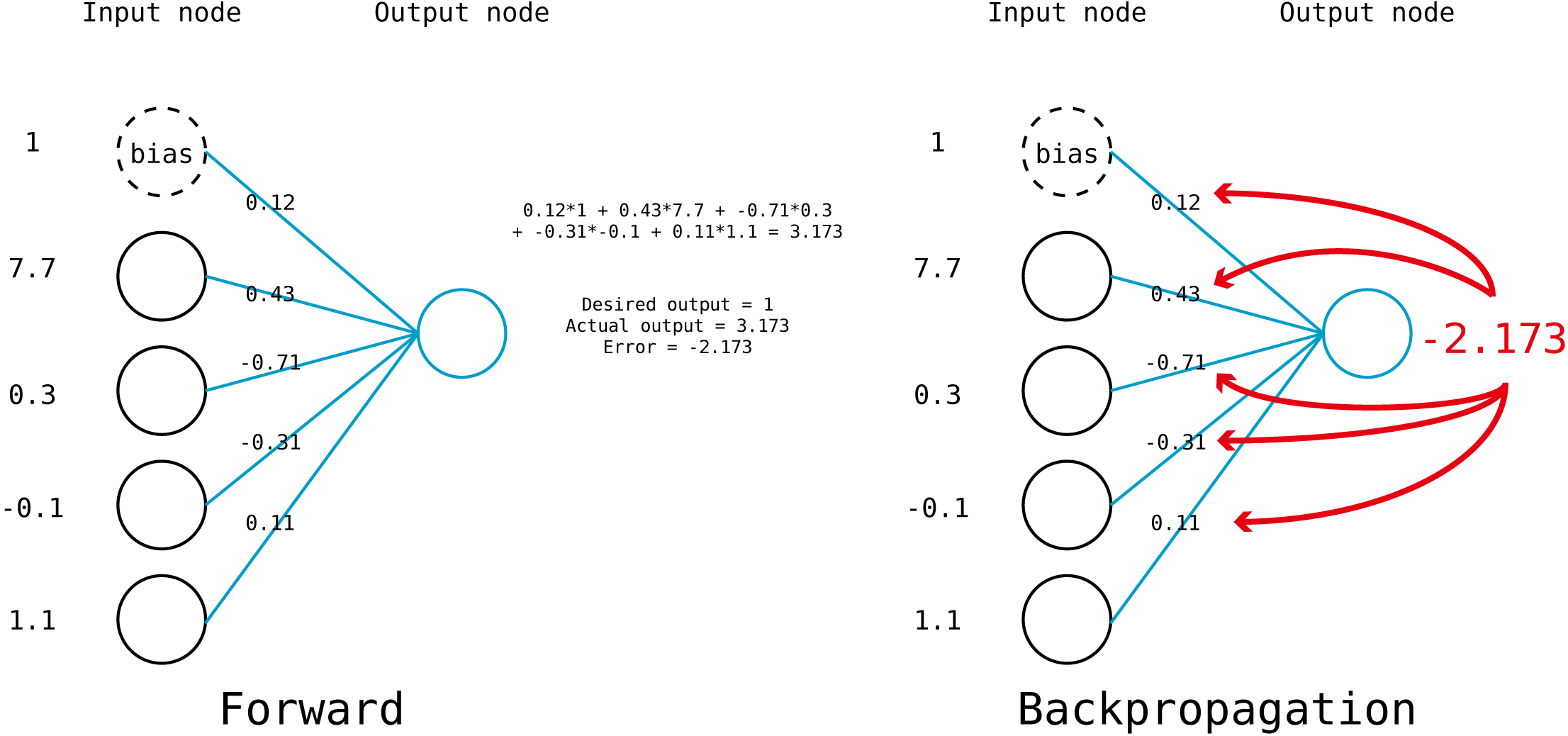
예로 위 처럼 input node가 총 4개 있는 perceptron은 총 5개의 weight 값(4+1)가질 것이다.
feedforward 계산에 의해서 actual output은 3.173이 나왔다.
desired output이 1이라고 할 때 위의 Error 정의대로라면 Error는 -2.173이 나오며 이는
"실제 나오는 값이 desired 보다 훨씬 크니, weight 값을 - 방향으로 움직여라(=줄여라)"
를 의미한다.
문제는 이 -2.173을 5개의 weight 값에 모두 동일하게 반영하면 안되고, input node의 값에 차등적으로 반영을 해야한다는 것이다.
Error를 만드는데 기여도가 높은 node의 weight 일 수록 weight 변경을 많이 해야한다.
bias를 제외한 첫 번째 node의 경우 7.7의 값이 들어왔다. 그에 비해서 두 번째 node는 0.3이 들어왔다.
당연히 저 -2.173이라는 큰 error 값에 기여한 부분이 첫 번째 node가 두 번째 node보다 크므로, 더 큰 값을 weight 에서 빼주어야 할 것이다.
어차피 learning rate 때문에 한번에 많은 양의 weight 변화가 생기지는 않을 것이므로, 이러한 Error의 기여도의 차이를 단순히 error에 input node의 값을 곱해주는 식으로 계산하면 편하다. 다음과 같이 말이다.
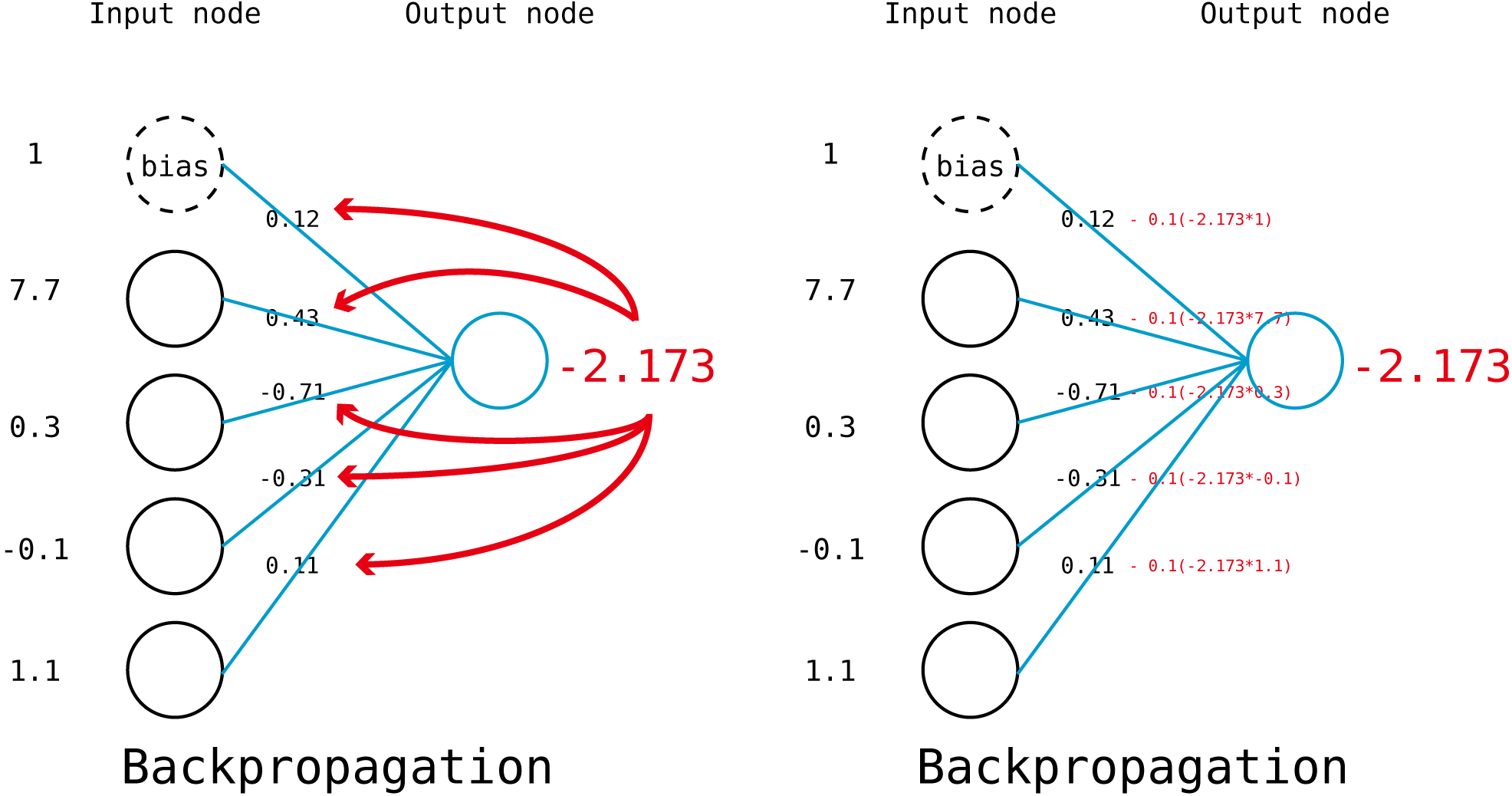
똑같은 짓을 k개의 perceptron에 대해 진행해야 하는데 이 역시 dot product로 할 수 있다.
살짝 편법이기는 하지만, 궁극적으로 우리가 알고 싶은건 (j +1 x k) 형태로 있는 weight의 각각의 원소에 얼마만큼의 값을 빼주어야 하는지 이므로 weight 변화량 또한 (j +1 x k)형태일것이다.
bias를 포함한 input node => (j+1 x 1)
Error => k x 1
원하는 형태 => (j +1 x k)
어떻게 dot product를 계산해야할지 알겠는가?
bias를 포함한 input node와 Error의 행과 열을 바꾼 값을 서로 dot product 해주면
(j+1 x 1) dot 1 x k =j +1 x k 가 된다.
import numpy as np
# Constants
num_input_node = 4
num_output_node = 3
learning_rate = 0.1
num_epoch = 100
# Variables
weights = np.random.rand(num_input_node + 1, num_output_node) * 2 -1
# rand 함수는 0~1 사이 값을 주기에 x2-1을 하면 -1과 1 사이의 값이 나온다.
# Feed Forward
input_node = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)
##############################여기부터##############################################
# Backpropagation
Error = desired_output - a
new_weights = weights - learning_rate*( np.dot(input_node, Error.T) )
이러한 과정을 모든 dataset에 대해서 epoch 번 만큼 반복해 주면 된다.
sklearn에 있는 가장 유명한 dataset인 iris 데이터를 사용해서 위의 모든 내용을 코드로 바꾸면 아래와 같다.
코드가 전부 돌아가면 정확도 값이 나올 것이다.
import numpy as np
from sklearn import datasets
data = datasets.load_iris()
X = data.data
y = data.target
# Constants
num_input_node = 4
num_output_node = 3
learning_rate = 0.01
num_epoch = 1000
# Variables
weights = np.random.rand(num_input_node + 1, num_output_node) * 2 -1
# rand 함수는 0~1 사이 값을 주기에 x2-1을 하면 -1과 1 사이의 값이 나온다.
for epoch in range(num_epoch):
for sample,target in zip(X,y):
# Make input node to column vector
x = np.reshape(sample, [4, -1])
# Feed Forward
input_node = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)
# Make desired output to column vector
desired_output = np.zeros([3,1])
desired_output[target] = 1
# Backpropagation
Error = desired_output - a
new_weights = weights + learning_rate*( np.dot(input_node, Error.T))
weights = new_weights
score = 0
for sample,target in zip(X,y):
# Make input node to column vector
x = np.reshape(sample, [4, -1])
# Feed Forward
input_node = np.vstack([[[1]], x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)
score += int(np.argmax(a) == target)
print(score / len(X))
이대로 코드를 짜면 정확도 값이 0.66을 넘기는 것을 본 적이 없다.
이는 개념의 단순화를 위해서 activation function을 쓰지 않았기 때문이다.
activation function을 쓰지 않으면 actual output 값이 한없이 크거나 작게 나오는 것이 가능하고, 이는 곧 한없기 크거나 작게 weight 값의 변경이 가능하다는 것이다.
실제로 위에서 learning rate 을 0.01로 사용했는데, 이보다 커지면 어느순간 최종 weight 값들이 inf (무한대)로 뜨기 시작한다.
activation function을 쓰면 극단적인 weight 변화라는 문제를 해결할 수 있지만, Error를 weight 값에 반영해 주는 방법을 바꿔주어야 한다.
여기서부터가 가장 어려운 개념이다.
Partial Derivative (편미분)과 Error
최대한 쉽게 설명하려고 노력하겠다.
우리가 결국 Perceptron을 만들면서 궁극적으로 원하는 것은 단 하나다.
Weight 값을 변화, 즉 증가시키거나 감소시켜서 Error를 줄이는 것
"변화" 라는 단어만 나오면 수학에서 바로 튀어 나오는 것이 바로 미분이다.
대체로 미분을 배울때 미분을 계산하는 부분에 많은 시간을 써서 그런지 미분이 의미하는 것을 잊는 경우가 있다.
특정 함수 f(x)를 미분해서 새로운 함수 f'(x)를 만들고, x에 특정한 값, 예를들어 3, 을 넣어주면 f(x) 함수의 숫자 3에서의 기울기를 알려준다.
f'(3)이 양수이면, f(3)인 지점에서 기울기가 오른쪽으로 증가한다는 뜻이니, f(3+아주 작은 수)의 값이 f(3)보다 클 것이다.
반대로 음수이면, f(3+아주 작은 수)의 값이 f(3)보다 작을 것이다.
만약에, X축이 weight, Y축이 Error인 아래의 좌측과 같은 그래프가 있다면 가장 적절한 weight 값은 어디일까?

당연히 중심부근에 있는 Error가 가장 작아지는 지점이다.
하지만 이런 그래프를 쉽게 그릴 수 있었다면 고등학교 2학년 방학숙제로 알파고를 만드는 내용이 나갔을 것이다.
대신 만약에 오른쪽과 같이 특정 weight 지점에서 weight-Error 그래프의 기울기라도 알 수 있으면 어떨까?
위의 예처럼 그래프의 기울기가 양수라면, weight을 증가시키면 Error가 증가하니 weight 값을 살짝 감소시키면 적어도 지금보다는 Error가 작아질 것이라고 확신할 수 있다.
또한 weight 값을 얼마나 감소 시켜야 할지도 대략 알 수 있다.
아래의 그림 모두 미분값의 기울기가 음수라 weight을 증가시키는 것이 Error를 낮출 가능성이 높다.
어느 경우 weight를 더 많이 증가시켜야 할까?

좌측의 경우 weight이 커지면 슬슬 그래프가 평평해질 것 같다.
그에 비해서 우측의 경우는 신나게 아래로 내려가는 중인 것 같다.
이런 경우 우측의 경우 많이 weight 값을 증가시켜도 될 것 같지만, 좌측의 경우 너무 많이 weight 값을 증가시켰다가는 Error가 더 올라가버릴지도 모른다.
즉, weight은 Error를 weight로 미분한 값의 반대방향으로 움직어야 한다.
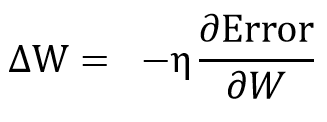
W의 변화량 = learning rate * (W에 대한 Error의 기울기) 의 반대
여기까지 이해가 되었다면 Error를 weight로 미분한 값만 알면 weight을 어떻게 바꿔야 할지 알 수 있다는 것을 눈치챘을 것이다.
기울기를 구하는 것이니 미분을 쓰면 될텐데, 편미분은 또 무슨 말일까?
편미분은 미분과 다른 것이 없다. 단지 미분을 하는데, 다른 변수는 다 무시해버리고 관심있는 변수로만 미분을 한다는 것이다.
예를들어 아래와 같은 수식이 있다고 하자.

함수 f는 x,y,z의 세 변수에 대한 복잡한 함수이다.
이를 x에 대해서 편미분을 하라는 것은 x 이외의 변수는 모두 상수로 보고 x에 대해서만 미분을 하면 된다.

참고로 편미분의 기호는 d 가 아닌 6을 거꾸로 쓴 듯한 기호로 표기한다.
편미분의 의미는 다른 변수들은 내 알 바 아니고 원하는 변수의 증감이 전체 함수의 기울기에 어떤 영향을 미치는지를 알려주는 것이다.
결론적으로 편미분 이야기를 꺼낸 이유는, weight의 변화에 따라 Error가 어떻게 달라지는지를 알기 위함, 즉, 아래의 값을 구하면 weight를 올릴지 내릴지 알 수 있다.
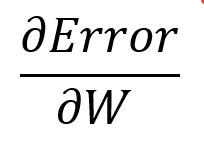
partial derivative의 또 다른 특성 중 하나는 chain rule 이다.
미분 가능한 함수들을 서로 연달아 배치해서 계산을 하는 방법인데, 수학적으로 말하자면 이 chain rule이 있기에 multi layer perceptron이 성립할 수 있다.

위와 같이 partial derivative 하나를 두 개로 쪼개서 계산할 수 있다.
그래서 SLP에 이를 적용해보자.
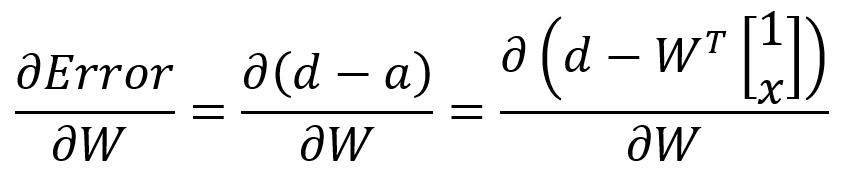
뭔가 이상하다.
저대로 가면 W가 있는 항이 우측 항 밖에 없으니 상수인 desired input은 W로 미분하면 사라진다.
Error function의 정의가 partial derivative 를 사용한 weight update방식에 맞지 않아서 그렇다.
desired output과 actual output의 차이의 제곱을 2로 나눈 것을 Error로 사용하기로 하면 문제가 해결된다.
어? 맘대로 Error function을 바꿔도 되나?
상관 없다. desired output과 actual output의 차이가 줄어들 수록 Error function의 값이 줄어들기만 하면 어떤 Error function을 써도 문제가 없다.
결과는 다음과 같다.

(d-a)는 Error, 그 뒤의 항은 input node의 값이다.
정확하게 우리가 위에서 본 식이다.
눈치챘을 수도 있지만 Error function 앞에 붙여둔 1/2는 정말 아무 의미없는 숫자다. (1/100 로 해도 된다.)
대신 1/2로 해두면 미분할 때 위에 있던 2가 똑 떨어져 나오기 때문에 위처럼 식이 깔끔해질 수 있다.
Single Layer Perceptron - with activation function
activation function은 input node와 각각의 weight 들의 곱의 합, 즉 a 값이 특정 범위 내에 있도록 해주는 함수이다.
가장 많이 사용하는 함수는 sigmoid, tanh, ReLU function 이며 output node의 값이 극단적으로 나오지 않도록 제한해주는 역할을 한다.

X 값에 따라 제한된 범위에서 Y값이 나오도록 하는 것 외에 activation function에는 한가지 요구사항이 붙는다.
바로 미분 가능성이다.
미분이 가능해야 나중에 partial derivative를 구할 수 있기에 위의 세 그래프 모두 X에 대해서 미분이 가능하다.
이 이후로 부터는 activation function으로 sigmoid 함수를 사용하도록 하겠다.

이 sigmoid 함수는 미분을 하면 재미있는 모습을 보여주는데, sigmoid 함수 y=f(x)는 미분을 하면 y(1-y) 로 표현이 된다.
미분하기 전 값으로 미분 후의 값을 표현할 수 있는 것이다.

위에서 언급한 tanh 함수도 미분을 하면 자기 자신으로 표현을 할 수 있으며, 이런 특성은 이후 아주 편리하다.
Feed Forward 계산
activation function이 없는 경우와 똑같다.
단지 node와 weight의 dot product를 바로 output으로 쓰는 것이 아니라 이 값을 activation function에 집어넣어서 나온 값을 output으로 사용한다.
아래에서 각 node의 weighted sum을 구한 뒤, sigmoid 함수에 넣어서 0.9598 이라는 값을 뽑아내는 것을 볼 수 있다.
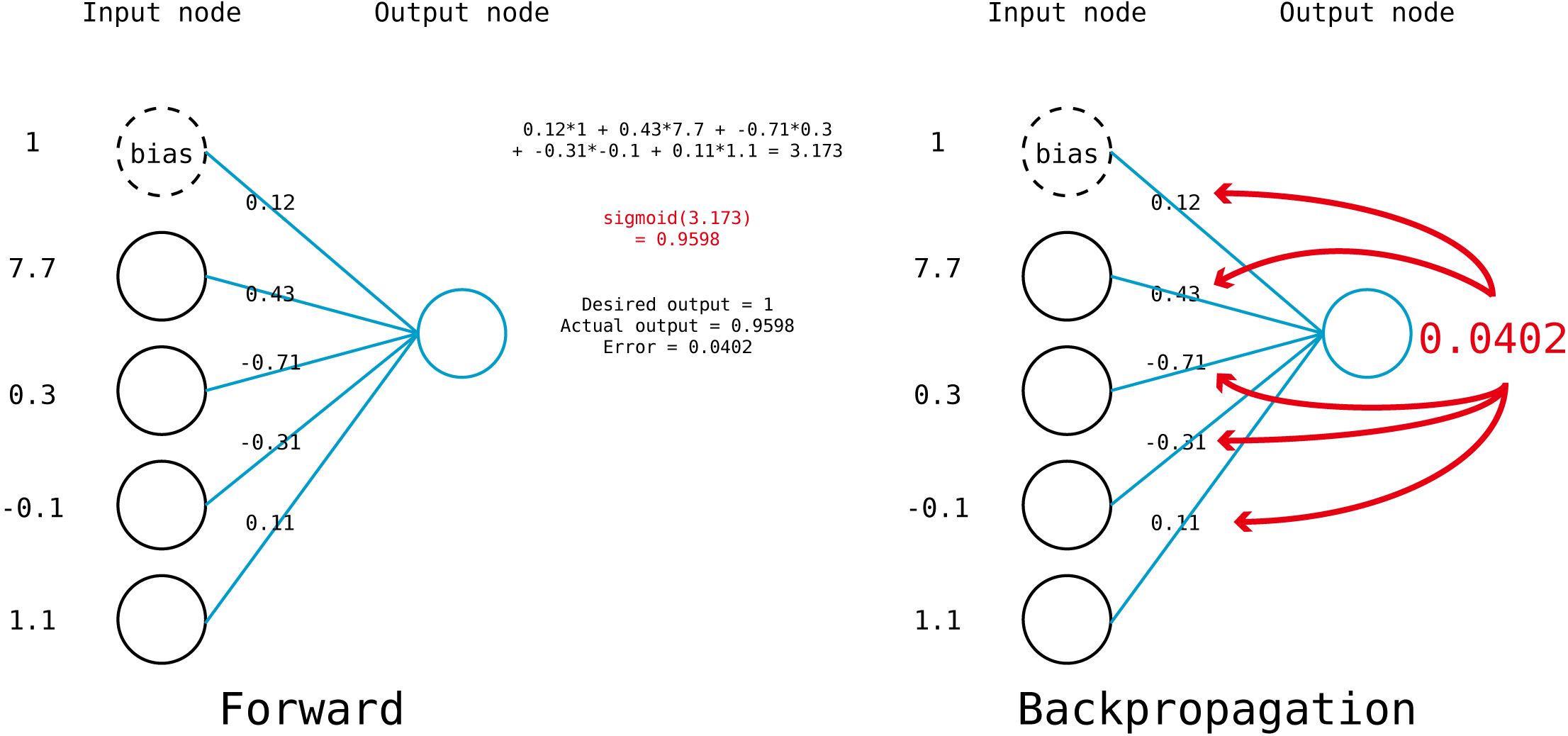
위에서 사용한 코드의 맨 아래 한 줄만 추가하면 feed forward 파트는 끝이다.
import numpy as np
# Constants
num_input_node = 4
num_output_node = 3
learning_rate = 0.1
num_epoch = 100
# Variables
weights = np.random.rand(num_input_node + 1, num_output_node) * 2 -1
# rand 함수는 0~1 사이 값을 주기에 x2-1을 하면 -1과 1 사이의 값이 나온다.
# Feed Forward
input_node = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)
##############################여기부터##############################################
output_node = 1 / (1+np.exp(a))Backpropagation 계산
위에서 언급한 partial derivative를 쓰면 Error에 대한 weight의 영향을 아래처럼 계산할 수 있다.
참고로 a는 input node에 각각 해당하는 weight 값을 곱하고 합한 값
y는 이 a를 activation function을 통과한 값이다.
x에 weight을 곱하고 합하기(=a). 이 결과를 sigmoid 함수에 넣기(=y)

마지막 식을 차원에 맞춰서 정렬한 후, 코드로 바꾸면 아래와 같다.
import numpy as np
# Constants
num_input_node = 4
num_output_node = 3
learning_rate = 0.1
num_epoch = 100
# Variables
weights = np.random.rand(num_input_node + 1, num_output_node) * 2 -1
# rand 함수는 0~1 사이 값을 주기에 x2-1을 하면 -1과 1 사이의 값이 나온다.
# Feed Forward
input_node = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)
output_node = 1 / (1+np.exp(a))
##############################여기부터##############################################
# Backpropagation
delta = -(desired_output - output_node) * output_node * (1-output_node)
new_weights = weights + learning_rate*( np.dot(delta, input_node.T).T )
코드 중간에 delta 라는 변수를 따로 만들고 나중에 bias를 포함한 input node의 값을 곱해주었다.
이를 반영해서 돌아가는 iris 코드는 다음과 같다.
import numpy as np
from sklearn import datasets
data = datasets.load_iris()
X = data.data
y = data.target
# Constants
num_input_node = 4
num_output_node = 3
learning_rate = 0.1
num_epoch = 1000
# Variables
weights = np.random.rand(num_input_node + 1, num_output_node) * 2 -1
# rand 함수는 0~1 사이 값을 주기에 x2-1을 하면 -1과 1 사이의 값이 나온다.
for epoch in range(num_epoch):
for sample,target in zip(X,y):
# Make input node to column vector
x = np.reshape(sample, [4, -1])
# Feed Forward
input_node = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)
output_node = 1 / (1 + np.exp(-a))
# Make desired output to column vector
desired_output = np.zeros([3,1])
desired_output[target] = 1
# Backpropagation
delta = -(desired_output - output_node) * output_node * (1-output_node)
new_weights = weights - learning_rate*( np.dot(delta, input_node.T).T)
weights = new_weights
score = 0
for sample,target in zip(X,y):
# Make input node to column vector
x = np.reshape(sample, [4, -1])
# Feed Forward
input_node = np.vstack([[[1]], x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)
output_node = 1 / (1 + np.exp(-a))
score += int(np.argmax(output_node) == target)
print(score / len(X))Multi Layer Perceptron
편미분과 말도 안되는 선형대수를 뚫고 위 까지 이해를 했다면, MLP도 정말 쉽게 넘어갈 수 있다.
중간에 back propagation에 한 스텝이 추가될 뿐이다.
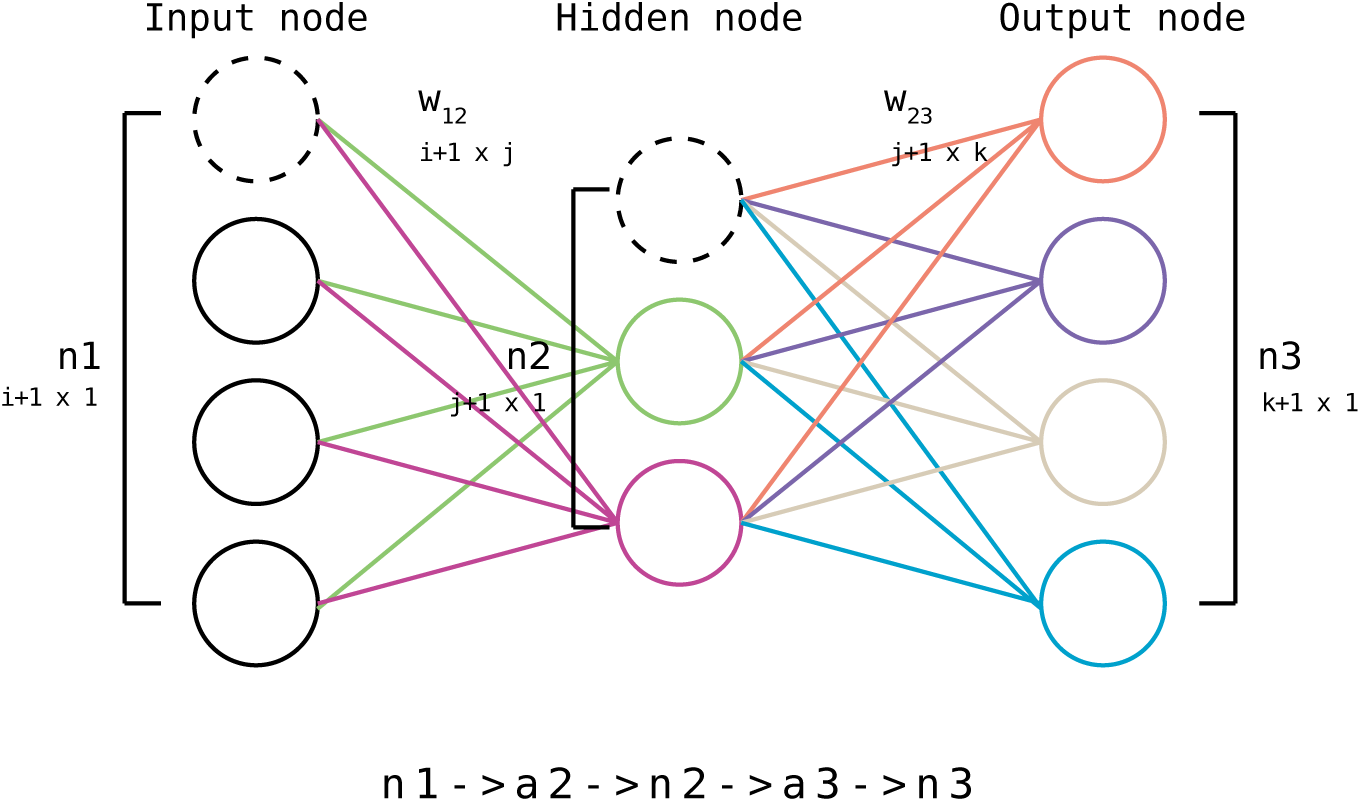
node가 총 3개가 되고 이에따라 weight matrix도 두개가 필요하다.
input, hidden, output으로 명명하면 혼돈의 여지가 있어서 순서대로 n1, n2, n3로 명명하고 weight 들은 첨자로 어느 노드 사이에 있는 weight 인지 달아두었다.

Feed Forward 계산
import numpy as np
# Constants
num_n1_node = 4
num_n2_node = 3
num_n3_node = 4
learning_rate = 0.1
num_epoch = 100
# Variables
W_12 = np.random.rand(num_n1_node + 1, num_n2_node) * 2 - 1
W_23 = np.random.rand(num_n2_node + 1, num_n3_node) * 2 - 1
# Feed Forward
n1 = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a2 = np.dot(W_12.T, n1)
n2 = 1 / (1 + np.exp(-(a2)))
n2 = np.vstack(([[1]], n2))
a3 = np.dot(W_23.T, n2)
n3 = 1 / (1 + np.exp(-(a3)))
Backpropagation 계산
W23의 계산

W23은 output node인 n3와 직접 연결되어 있기에 Single Layer 처럼 구하면 된다.
문자들만 달라졌지 위에서 작성한 식과 똑같다.
W12의 계산
W23의 경우는 바로 output node와 연결이 되어 있어서 어느 부분을 고치면 되는지 직관적으로 알 수 있는데, W12의 영향력은 W23을 한번 더 지나서 나타나기에 중간 연결고리를 모른다.
대신 우리는 각각의 값들의 아래의 연결고리를 안다.

a2랑 W12가 같이 있는 식이 있고, a2 & n2 | n2 & a3 | a3 & n3 | Error 와 n3가 같이 있는 식도 알고 있다.
따라서 이러한 연결구조를 활용해서 chain rule을 통해 아래의 식을 구할 수 있다.
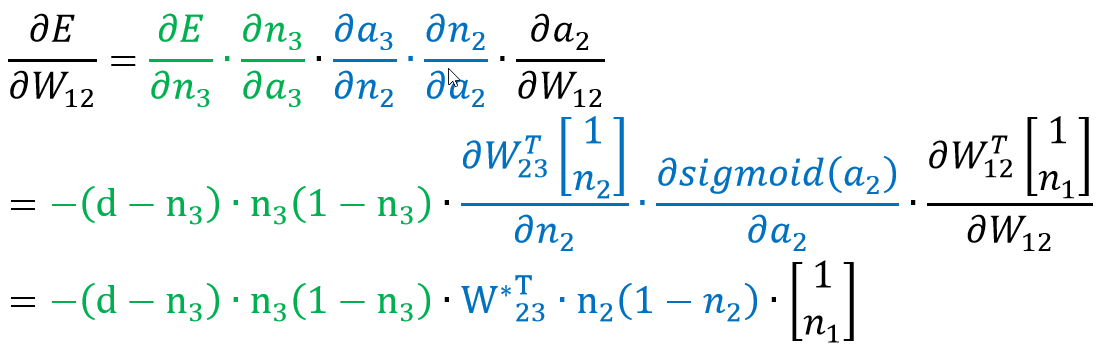
마지막 식의 첫 파란 항에서 W23 위에 *이 붙어있는데, 이는 첫째행을 제외한 W23을 말한다.
이 행을 지워주는 이유는 두 가지 방법으로 설명할 수 있는데,
일단, 편미분을 bias를 포함한 n2로 하는 것이 아니라 n2로만 하기에 Weight에서 bias 관련 부분을 빼고 나머지 값만 써주는 것이라고 설명할 수 있다.
다른 방법으로는 W23의 첫째 행에는 n2의 bias와 n3를 연결하는 weight 값이 들어있는데, n1과 n2의 bias는 서로 연결되어 있지 않으므로 n2의 bias 관련 정보는 빼주는 것이라고도 설명할 수 있다.

겨우 끝났다.
이 모든 과정을 코드로 정리하면 아래와 같다.
import numpy as np
# Constants
num_n1_node = 4
num_n2_node = 3
num_n3_node = 4
learning_rate = 0.1
num_epoch = 100
# Variables
W_12 = np.random.rand(num_n1_node + 1, num_n2_node) * 2 - 1
W_23 = np.random.rand(num_n2_node + 1, num_n3_node) * 2 - 1
# Feed Forward
n1 = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a2 = np.dot(W_12.T, n1)
n2 = 1 / (1 + np.exp(-(a2)))
n2 = np.vstack(([[1]], n2))
a3 = np.dot(W_23.T, n2)
n3 = 1 / (1 + np.exp(-(a3)))
##############################여기부터##############################################
# Backpropagation
delta23 = -(desired_output - n3) * n3 * (1-n3)
W_23 = W_23 - learning_rate * np.dot(delta_23, n2.T).T
# 위에서 n2 변수를 bias를 포함해서 정의했기에 여기서는 [1:,:] 인덱싱을 사용해 맨 윗행 값을 뺀다.
# 또한 W_23에서도 맨 윗행 값을 뺀다.
delta_12 = np.dot(W_23[1:, :], delta_23) * n2[1:, :] * (1 - n2[1:, :])
W_12 = W_12 - learning_rate * np.dot(delta_12, n1.T).T
iris 데이터에 적용한 코드는 아래와 같다.
import numpy as np
from sklearn import datasets
from sklearn import model_selection
data = datasets.load_iris()
X = data.data
y = data.target
# Select node
num_n1_node = 4
num_n2_node = 12
num_n3_node = 3
# Generate model
W_12 = np.random.rand(num_n1_node + 1, num_n2_node) * 2 - 1
W_23 = np.random.rand(num_n2_node + 1, num_n3_node) * 2 - 1
num_epoch = 1000
learning_rate = 0.2
for epoch in range(num_epoch):
for sample, target in zip(X,y):
# Forward
n1 = np.reshape(np.append([1], sample), [num_n1_node + 1, -1])
a2 = np.dot(W_12.T, n1)
n2 = 1 / (1 + np.exp(-(a2)))
n2 = np.vstack(([[1]], n2))
a3 = np.dot(W_23.T, n2)
n3 = 1 / (1 + np.exp(-(a3)))
# Backward
DesiredOutput = np.zeros([num_n3_node, 1])
DesiredOutput[target] = 1
Error = 0.5 * (DesiredOutput - n3) ** 2
delta_23 = -(DesiredOutput - n3) * n3 * (1 - n3)
W_23 = W_23 - learning_rate * np.dot(delta_23, n2.T).T
delta_12 = np.dot(W_23[1:, :], delta_23) * n2[1:, :] * (1 - n2[1:, :])
W_12 = W_12 - learning_rate * np.dot(delta_12, n1.T).T
score = 0
for sample, target in zip(X,y):
n1 = np.reshape(np.append([1], sample), [num_n1_node + 1, -1])
y1 = np.dot(W_12.T, n1)
n2 = 1 / (1 + np.exp(-(y1)))
n2 = np.vstack(([[1]], n2))
y2 = np.dot(W_23.T, n2)
n3 = 1 / (1 + np.exp(-(y2)))
score += int(np.argmax(n3) == target)
print(score / len(X))아직 이것보다 더 쉽게 Multi Layer Perceptron을 설명하는 글을 보지 못했다.
Multi layer를 도입하기 위해서는 partial derivative 개념은 필수이며, 2차원 weight matrix에 대한 연산을 설명하기 위해서는 Sigma로 도배하거나, 선형대수로 머리를 터뜨려야 한다.
그나마 선형대수를 사용하는 것이 겉으로 보기에 아주 깔끔하고 정돈되어 있어서 굳이 이 방법을 사용했다.
하나 고백하자면 matrix와 matrix의 partial derivative는 제대로 정의가 되어있지 않다고 한다. (wiki 참고)
따라서 matrix calculus를 제대로 배운 사람이라면 말도 안되는 transpose, 맘대로 어기는 Commutative property에 혀를 찰 것이며 제대로 계산을 하기 위해서는 다른 방법을 써주어야 하는 것 같다.
matrix calculus 부분은 다음을 위한 과제로 남겨두려고 한다.
어찌되었건, dimension만 제대로 맞춰주면 위의 코드는 돌아간다!
마치며
기계학습에 대한 대중들의 관심이 높아져서 그런지 관련 사기꾼들도 같이 늘어나는 것 같다.
내 연구 프로젝트에 대해서 생뚱맞게 4차 산업혁명이나 인공지능과 관련있는 점이 있냐고 물어보는 사람들이 있는가 하면, 기계학습과 인공지능의 차이도 모르는 사람들이 아무곳에나 "자율형", "인공지능" 등의 말을 붙이고 다닌다.
물론, 어떠한 학문이든 진입 장벽은 낮을수록 좋고, 누구나 쉽게 분야에 참여해 배워보고, 그 유용성을 누려야 한다고 생각한다.
하지만 가상악기와 MIDI를 사용해서 바이올린을 연주하는 사람이 "나는 바이올린을 잘 안다!" 라고 말하면 안되듯이 남이 만들어 놓은 코드 몇 줄로 classifier를 만들고 기계학습을 잘한다고 말하면 안된다.
더욱이 기계학습을 연구에 사용하거나, 실무에 사용하는 경우 적어도 기저 개념을 한번이라도 유도해보지 않으면 주의점과 한계들을 놓쳐서 치명적인 오류를 범할 수 있을 것이다.
자신과 관련된 분야에 대중의 관심이 많아질 수록, 보다 겸손하고 신중한 자세를 취하는 것이 옳은 것 같다.
- 부족한 글 읽어주셔서 감사합니다.
- 오류나 오타가 있으면 댓글로 감사히 받겠습니다.
'취미 > Programming' 카테고리의 다른 글
| [Vim] Linux 상에서의 Not an editor command: ^M 문제 (0) | 2021.03.24 |
|---|---|
| Python(anaconda) Vim intagration (2) | 2020.10.28 |
| [GitHub] 3. GUI Git: GitHub Desktop, Sourcetree, GitKraken (0) | 2019.11.13 |
| [GitHub] 2. git과 GitHub의 관계 (0) | 2019.11.12 |
| [GitHub] 1. 시작하기 (0) | 2019.11.11 |
이 시리즈를 포스팅하게 된 계기는 한달전부터 Ubuntu 를 사용을 시작한 것이다.
vim과 터미널 명령어들을 배우면서 슬슬 GUI보다 CUI에 익숙해지고 있어서 git도 이제 GUI 프로그램을 사용하지 않고 명령어를 외어서 사용하려는 중이다. 하지만 git에 입문하는 처음이라면 꼭 GUI 프로그램을 사용해라.하는 것을 추천한다.
대체 누가 git 입문 책에서 CUI로 알려주는지. git은 꼭 GUI로 시작해라.
처음에는 branch라는 개념이 직관적으로 다가오지 않으며, 여러 branch가 꼬이기 시작하면 머리도 같이 꼬일 수 있다.
또한 아무리 CUI가 입력하기엔 편해도 visualize 하는 면에 있어서는 GUI를 이길 수 없다. 나는 CUI에 익숙해져도 GUI git을 지우지는 않을거라고 확신한다.

GUI로 git을 사용할 수 있게 해주는 프로그램은 그렇게 많지 않다.
처음에는 GitHub에서 자체제작한 GitHub Desktop을 사용했는데 깔끔한 그래픽의 군더더기 없는 디자인이라 마음에 들었지만 git의 모든 기능을 구현하지 않은 것 같고, 전반적으로 UI가 휑한 느낌을 주었다.
단순한 기능들만 사용한다면 추천하기는 한다.

이후로 본격적으로 git을 사용하게 만든 장본인은 Sourcetree이다. GitHub Desktop과는 다르게 다양한 기능들을 구현을 해두었고, 구현한 기능들에 비해 디자인도 깔끔하게 만들어서 한동안은 정말 잘 썼으나... 2016년즈음 자꾸 내부 프로그램 문제가 발생해서 설치-재설치, GitHub Desktop으로 갈아탔다 다시 오기를 몇 번.. 아주 지쳐버렸다.
지금은 그래도 그때보다는 더 안정화 되어있을 것이다. 하지만 돌아갈 생각은 없다.

시커먼 화면을 좋아해서 그런지 한번 적응하고 나서부터는 바꿀 생각을 전혀 안하고 있다.
UI는 위의 두 프로그램의 딱 중간정도지만 복잡한 기능들도 다 구현이 되어있고 아직까지 한번도 크래시가 난적이 없다.
의외로 이 프로그램에 대한 소개가 별로 없는 것 같기에 프로그램에 대한 애정을 담아 이후 포스팅부터는 이 프로그램을 기준으로 설명하겠다.

2017년 이후 거의 3년간 문제없이 쓰고 있는 것은 GitKraken이다.
마무리
아마 직접 git을 설치하는 일은 없을 것이다. 혹시 리눅스 유저라면 이미 git이 기본으로 깔려있을 것이고, 윈도우 유저라면 바로 GUI 프로그램인 GitKraken을 깔자. 이 프로그램 역시 학생에게 무료로 Pro 버전을 제공한다.
https://www.gitkraken.com/student-resources
Free Developer Tools for Students | GitKraken
Students can get a GitKraken Pro account free as part of the GitHub Student Developer Pack. The Git GUI client makes learning Git easier by providing a visual, intuitive experience. Glo Boards are great for working with student teams to track project progr
www.gitkraken.com
이전 포스트에서 GitHub에 가입을 하고, 이번 포스트에서 GitKraken을 설치했다면 이제 준비는 끝이다.
다음 포스트부터 바로 실제 git에 구조와 사용법에 대해서 작성하도록 하겠다.
'취미 > Programming' 카테고리의 다른 글
| Python(anaconda) Vim intagration (2) | 2020.10.28 |
|---|---|
| Multi Layer Perceptron (MLP) (1) | 2020.05.06 |
| [GitHub] 2. git과 GitHub의 관계 (0) | 2019.11.12 |
| [GitHub] 1. 시작하기 (0) | 2019.11.11 |
| 에어컨 냉각수 수위 경보기 (0) | 2019.07.26 |