'2020/05'에 해당되는 글 1건
- 2020.05.06 Multi Layer Perceptron (MLP) 1
처음 Perceptron의 개념을 접한지 벌써 6년이 지났다.
당시 Single Layer Perceptron (SLP)만 배웠었는데 신경망의 작동원리를 표방한 구조가 마음에 들어 다른 서적까지 뒤져가며 개념을 이해하려고 애썼다.
선형대수도 제대로 알지 못했는데 구조가 단순해서 그런지 수학적으로 완벽하게 개념을 이해할 수 있었다.
과제로 나온 문제 중 하나가 '왜 SLP는 XOR 문제를 풀지 못하는지 설명하라' 였는데 이에 대해서 완벽한 답을 내놓았을 때의 짜릿함이란...
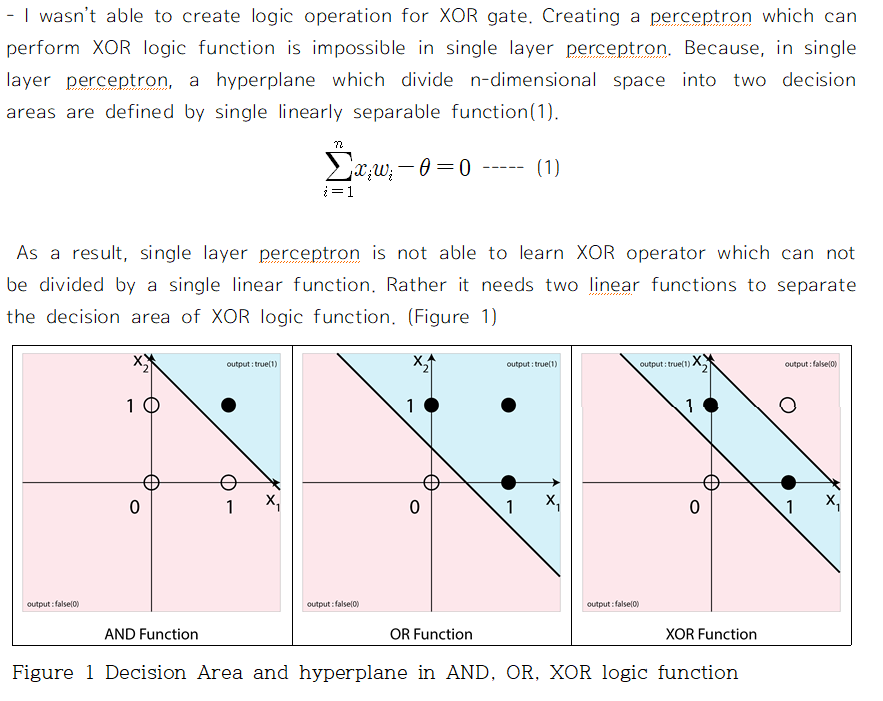
SLP는 그 이후로도 다른 수업이나 특강에서 접할 기회가 많아서 익숙해졌지만 , 아직까지 Multi Layer Perceptron (MLP)를 완벽하게 이해하지 못했다. 수식을 외워서 어찌저찌 코드를 짤 수는 있었지만 왜 저런 수식이 나오는지 개념적으로 설명을 하지 못했다.
지난 코드들을 정리하던 중 짜다 포기한 MLP 코드가 있길래 지금이라면 이해할 수 있지 않을까 하고 도전한 결과, 드디어 오랫동안 끝내지 못한 과제를 해결하게 되었다.
이해한 개념을 잊지 않도록 SLP부터 정리하고 기록하려고 한다.
Single Layer Perceptron
Perceptron 구성에 필요한 것
- input node의 수
- output node의 수
- 초기 weight 값
- learning rate
- epoch 수
먼저 network를 구성하기 위해서 필요한 것은 input node와 output node의 숫자다.
input node의 수 : j
output node의 수 : k
일반적으로 "한 개"의 perceptron은 여러 개의 input을 받아서 하나의 output을 출력하는 대상을 말하기에 output node가 k개 있는 위의 예에서는 k개의 perceptron이 하나로 합쳐져 있는 것이라고 생각해야 한다.

또 필요한 것은 사실상 학습이 일어나는 변수인 weight의 초기값이다.
위와 같이 모든 node 들이 서로 연결된 fully-connect 조건인 경우 input node의 수 x output node의 수 (j x k) 만큼 weight 값이 필요하다.
Output node에서는 이후 input node의 값들을 각각의 weight로 곱해주고 threshold를 넘냐 안넘냐로 output을 바꾸는데 이게 꽤 귀찮다.
왜냐하면 이 threshold를 잘못 정하면 학습이 전혀! 일어나지 않기 때문이다.
그래서 사용하는 방법이 input node가 비록 j개만큼 있지만 항상 1 값을 내놓는 가상의 node를 만들고 weight의 수를 (j x k)가 아닌 (j+1 x k) 로 설정하는 것이다.
이러면 모든 output node의 threshold를 0으로 설정해도 이 가상의 node를 통해 threshold 값이 조정된다.
이러한 가상의 node를 bias 라고 한다.

이렇게 하면 나중에 weight update를 할 때 weight 값이 바뀌면서 각각의 node의 threshold가 바뀌게 되고, 각 node 별로 최적의 threshold가 구해질 것이다.
weight matrix : W => (j +1 x k)
초기 weight 값을 구하는 것에는 다양한 방법이 있으나 편의상 -1과 1 사이의 무작위 값으로 쓰도록 하자.
마지막으로 매번 학습마다 weight 값을 얼마만큼 바꿀지에 대한 learning rate (보통 0.1 정도면 충분) 와 전체 training sample을 몇번 돌려가며 학습을 시킬지에 대한 epoch ( 일단 100정도) 이 필요하다.
import numpy as np
# Constants
num_input_node = 4
num_output_node = 3
learning_rate = 0.1
num_epoch = 100
# Variables
weights = np.random.rand(num_input_node + 1, num_output_node) * 2 -1
# rand 함수는 0~1 사이 값을 주기에 x2-1을 하면 -1과 1 사이의 값이 나온다.Feed Forward 계산
j+1개의 값들을 각각의 weight들과 곱한 뒤, 합하는 작업을 총 perceptron의 수인 k번 해야한다.
물론 Method 1처럼 for 문을 두 번 사용하면 해결이 되겠지만 Method 2처럼 코드 한줄로 모든 연산을 끝낼 수 있다.
바로 선형대수를 이용하는 것이다.
# Method 1
for perceptron in range(k):
for node in range(j+1):
output_node[perceptron] += weight[node, perceptron] * input_node[node]
# Method 2
output_node = np.dot(weight.T, input_node)
대학원 인공지능개론 수업에서는 교수님이 학생들이 전부 선형대수를 완벽히 알고있다고 가정하고 설명을 하시던데 물리/정보계 이과가 아니어서 그런지 나는 고등학교때 행렬 연산 지식이 전부다.
이 수업을 따라가려고 선형대수로 유명하다는 Strang 교수님의 선형대수 책 스터디도 진행을 했는데 정작 머릿속에 남아있는 개념은 딱 두 가지이다.
행렬의 곱, dot product와 dot product 에서의 차원 계산
1. The dot product (행렬의 곱)
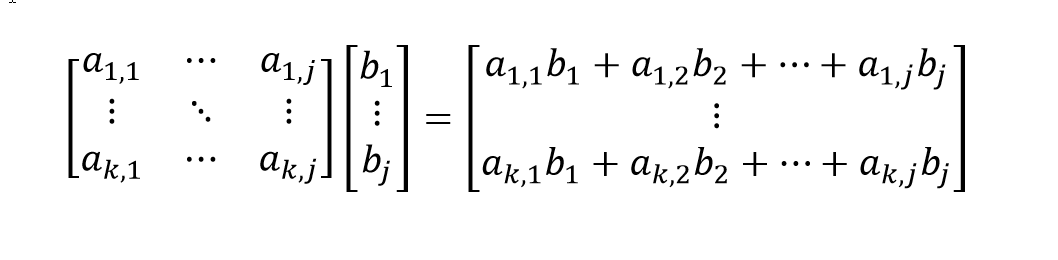
k x j 형태의 matrix와 j x 1 형태의 matrix (혹은 columnar vector) 의 Dot product는 위와 같이 계산된다.
복잡해보이지만 좌측 matrix의 한 행의 원소들(총 j개)를 각각 같은 위치에 있는 우측 matrix의 열의 원소들(총 j개)로 곱해준 뒤 이를 전부 합해주면 한 행의 element가 완성이 된다.
어짜피 하는 연산은 for 문 2개를 돌리는 것과 같지만, 이렇게 각각의 원소들을 다른 matrix의 대응하는 원소와 곱한뒤 이를 합하는 연산이 Perceptron 외에도 정말 자주 등장하기에 수학에서 이러한 연산을 dot product라고 따로 정의한 것 같다.
물리에서 벡터 연산이나 간단한 선형 방정식에서도 자주 본 적이 있다.
2. The dimension of the dot product
위에 언급한 부분을 잘 보면 두 matrix의 dot product를 구할 때 중요한 조건이 있다.
"좌측 matrix의 한 행의 원소들(총 j개)를 각각 같은 위치에 있는 우측 matrix의 열의 원소들(총 j개)로 곱해준 뒤 이를 전부 합해주면 한 행의 element가 완성이 된다."
바로 좌측 matrix의 열의 수와 우측 matrix의 행의 수가 일치해야 연산이 가능하다는 것이다.
또한 연달아 dot product를 계산하면 최종 결과는 최좌단 matrix의 행의 수 x 최우단 matrix의 열의 수 가 된다.
예를들어, matrix A, B, C가 각각 axb, bxc, cxd 의 차원을 가지고 이들은 전부 곱하면, 최종결과는 a x d가 된다.
이 개념이 아주 중요하다.
끽해야 2-3개의 행과 열로 된 matrix를 다루는 손으로 푸는 문제는 바로 어떻게 연산을 해야할지 보이는데, 수십, 수백개의 행과 열로된 matrix를 컴퓨터로 연산을 할 때는 matrix의 구조가 보이지 않아서 차원이 맞지 않는 오류가 나기 쉽다.
그래서 곱해야할 것들을 정하고, 원하는 결과의 차원을 정한뒤, matrix 자체는 보지 않고 matrix의 dimesion만 보면서 코딩을 해나간다.
다시 SLP로 돌아가서, 현재 weight은 (j +1 x k)로 되어있고, input node의 수는 j+1.
원하는 연산을 위해서는 weight matrix의 행과 열을 바꾸고 bias를 포함한 input node와 곱해주면 된다.
참고로 이렇게 행과 열을 바꿔주는 행위를 transpose 라고 하고 위에 작은 T 첨자를 붙인다.

처음 배울때 선형대수만큼 짜증나는 것은 없다!
덧셈과 곱셈만 있음에도 당장 위에 수식만 봐도 머리가 돌아버릴 것 같다.
그런데 저런 모든 과정을 ∑ 기호를 쓰지 않고 아래와 같이 단순한 기호로 표시할 수 있다는 것은 정말 큰 장점이다.

처음에만 위에 기나긴 수식을 하나 하나 따라가면서 이해하고, 그 이후로는 각 matrix의 차원만 봐도(얘가 j x k 인지 k x j 인지) 전혀 문제가 없으니 걱정 마시라!
우리가 해야할 부분은 dot product를 언제 써야하는지 아는 것과, dot product를 낼 두 matrix의 차원을 맞춰주는 것 뿐이다.
import numpy as np
# Constants
num_input_node = 4
num_output_node = 3
learning_rate = 0.1
num_epoch = 100
# Variables
weights = np.random.rand(num_input_node + 1, num_output_node) * 2 -1
# rand 함수는 0~1 사이 값을 주기에 x2-1을 하면 -1과 1 사이의 값이 나온다.
##############################여기부터##############################################
# Feed Forward
input_node = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)Backpropagation 계산
다음 단계는 총 k개의 perceptron마다 나온 a 값을 실제로 나와야 하는 값이랑 비교하는 것이다.
desired output의 d를 따서 d라고 부르겠다.
Error = desired output(d) - actual output(a)
a 값이 k x 1 의 형태로 나올 것이기에 desired output도 똑같이 모든 perceptron, 혹은 output node의 desired output 값을 column vector 화 해서 서로 빼주면 k x 1 의 형태로 error를 구할 수 있다.
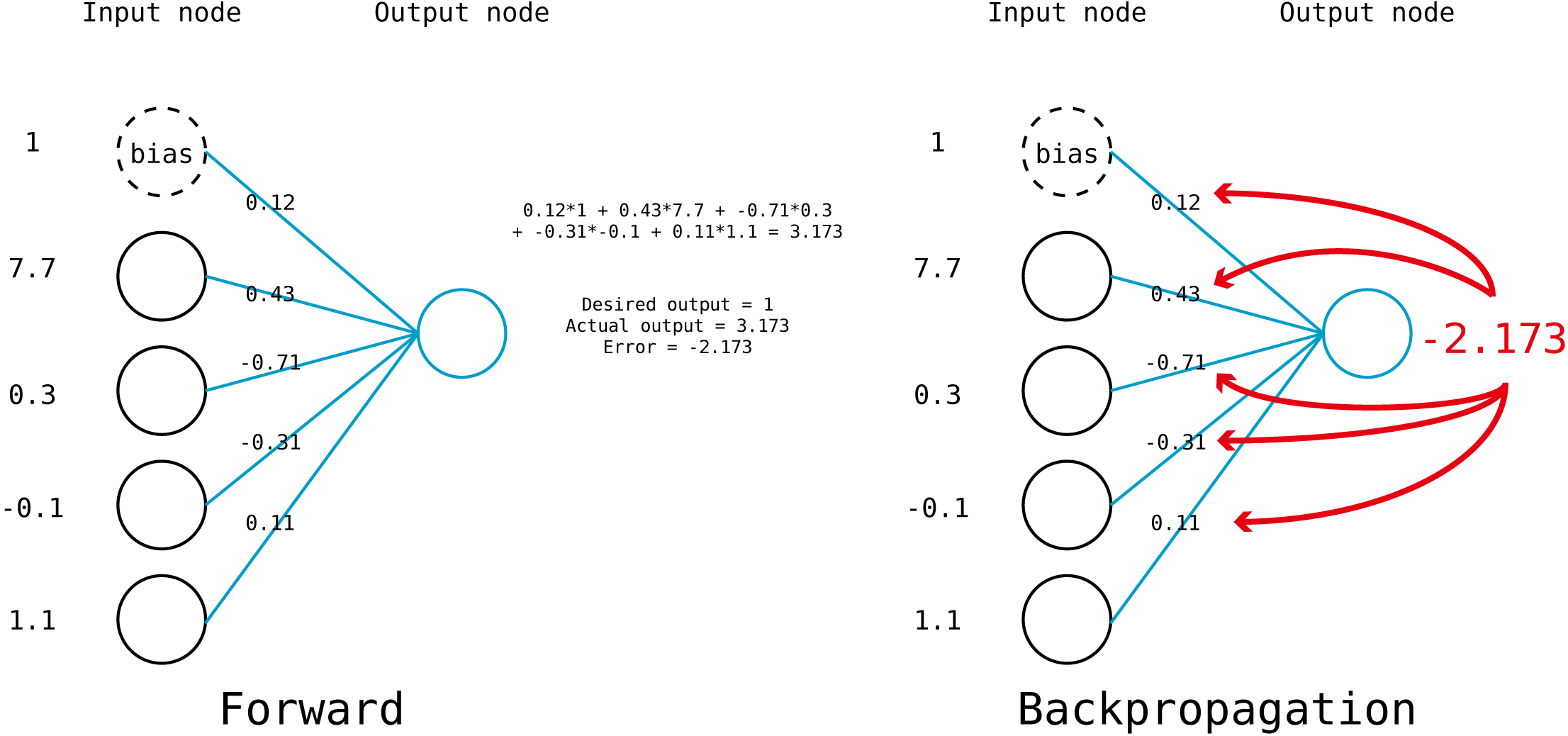
예로 위 처럼 input node가 총 4개 있는 perceptron은 총 5개의 weight 값(4+1)가질 것이다.
feedforward 계산에 의해서 actual output은 3.173이 나왔다.
desired output이 1이라고 할 때 위의 Error 정의대로라면 Error는 -2.173이 나오며 이는
"실제 나오는 값이 desired 보다 훨씬 크니, weight 값을 - 방향으로 움직여라(=줄여라)"
를 의미한다.
문제는 이 -2.173을 5개의 weight 값에 모두 동일하게 반영하면 안되고, input node의 값에 차등적으로 반영을 해야한다는 것이다.
Error를 만드는데 기여도가 높은 node의 weight 일 수록 weight 변경을 많이 해야한다.
bias를 제외한 첫 번째 node의 경우 7.7의 값이 들어왔다. 그에 비해서 두 번째 node는 0.3이 들어왔다.
당연히 저 -2.173이라는 큰 error 값에 기여한 부분이 첫 번째 node가 두 번째 node보다 크므로, 더 큰 값을 weight 에서 빼주어야 할 것이다.
어차피 learning rate 때문에 한번에 많은 양의 weight 변화가 생기지는 않을 것이므로, 이러한 Error의 기여도의 차이를 단순히 error에 input node의 값을 곱해주는 식으로 계산하면 편하다. 다음과 같이 말이다.
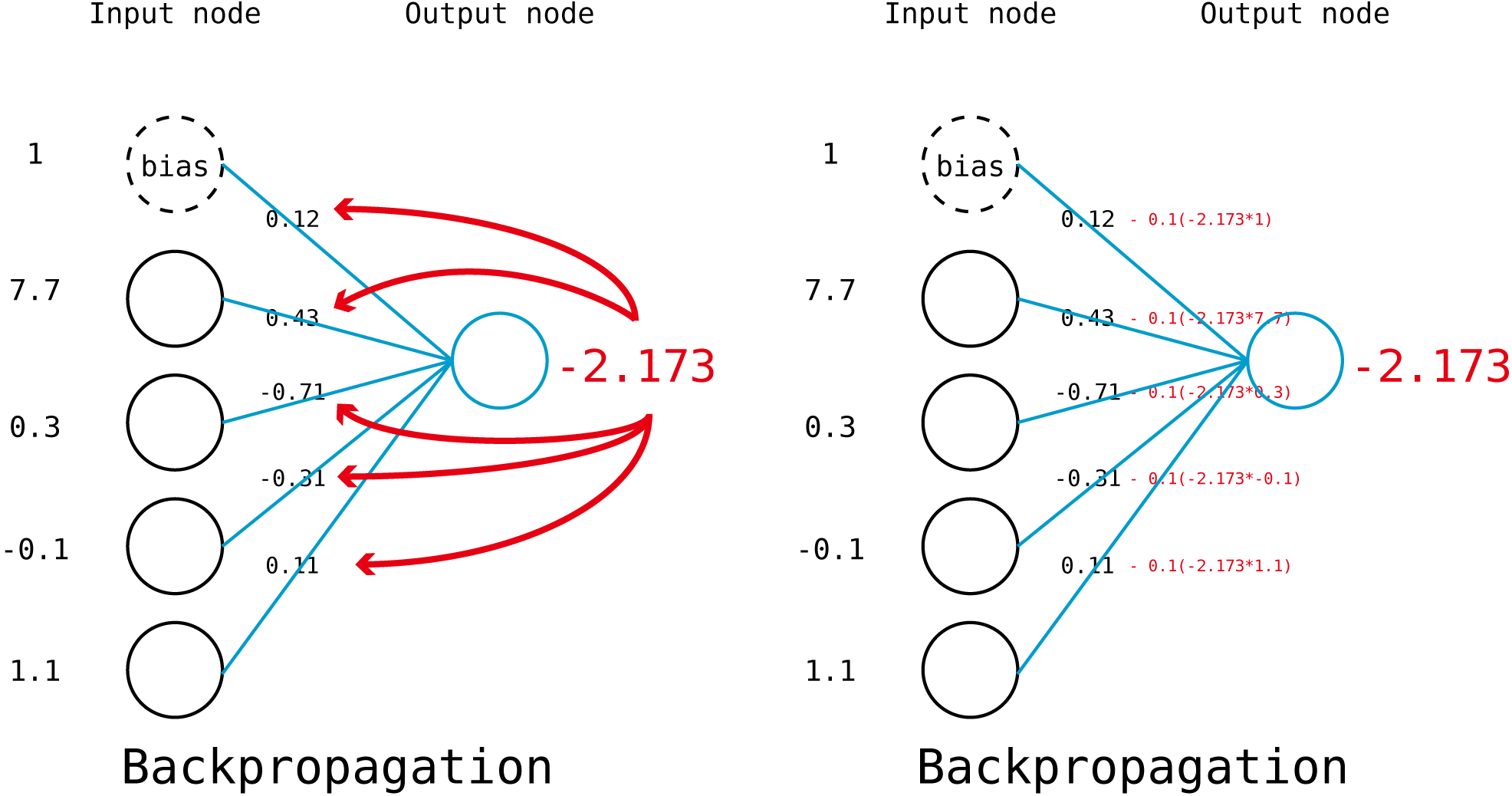
똑같은 짓을 k개의 perceptron에 대해 진행해야 하는데 이 역시 dot product로 할 수 있다.
살짝 편법이기는 하지만, 궁극적으로 우리가 알고 싶은건 (j +1 x k) 형태로 있는 weight의 각각의 원소에 얼마만큼의 값을 빼주어야 하는지 이므로 weight 변화량 또한 (j +1 x k)형태일것이다.
bias를 포함한 input node => (j+1 x 1)
Error => k x 1
원하는 형태 => (j +1 x k)
어떻게 dot product를 계산해야할지 알겠는가?
bias를 포함한 input node와 Error의 행과 열을 바꾼 값을 서로 dot product 해주면
(j+1 x 1) dot 1 x k =j +1 x k 가 된다.
import numpy as np
# Constants
num_input_node = 4
num_output_node = 3
learning_rate = 0.1
num_epoch = 100
# Variables
weights = np.random.rand(num_input_node + 1, num_output_node) * 2 -1
# rand 함수는 0~1 사이 값을 주기에 x2-1을 하면 -1과 1 사이의 값이 나온다.
# Feed Forward
input_node = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)
##############################여기부터##############################################
# Backpropagation
Error = desired_output - a
new_weights = weights - learning_rate*( np.dot(input_node, Error.T) )
이러한 과정을 모든 dataset에 대해서 epoch 번 만큼 반복해 주면 된다.
sklearn에 있는 가장 유명한 dataset인 iris 데이터를 사용해서 위의 모든 내용을 코드로 바꾸면 아래와 같다.
코드가 전부 돌아가면 정확도 값이 나올 것이다.
import numpy as np
from sklearn import datasets
data = datasets.load_iris()
X = data.data
y = data.target
# Constants
num_input_node = 4
num_output_node = 3
learning_rate = 0.01
num_epoch = 1000
# Variables
weights = np.random.rand(num_input_node + 1, num_output_node) * 2 -1
# rand 함수는 0~1 사이 값을 주기에 x2-1을 하면 -1과 1 사이의 값이 나온다.
for epoch in range(num_epoch):
for sample,target in zip(X,y):
# Make input node to column vector
x = np.reshape(sample, [4, -1])
# Feed Forward
input_node = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)
# Make desired output to column vector
desired_output = np.zeros([3,1])
desired_output[target] = 1
# Backpropagation
Error = desired_output - a
new_weights = weights + learning_rate*( np.dot(input_node, Error.T))
weights = new_weights
score = 0
for sample,target in zip(X,y):
# Make input node to column vector
x = np.reshape(sample, [4, -1])
# Feed Forward
input_node = np.vstack([[[1]], x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)
score += int(np.argmax(a) == target)
print(score / len(X))
이대로 코드를 짜면 정확도 값이 0.66을 넘기는 것을 본 적이 없다.
이는 개념의 단순화를 위해서 activation function을 쓰지 않았기 때문이다.
activation function을 쓰지 않으면 actual output 값이 한없이 크거나 작게 나오는 것이 가능하고, 이는 곧 한없기 크거나 작게 weight 값의 변경이 가능하다는 것이다.
실제로 위에서 learning rate 을 0.01로 사용했는데, 이보다 커지면 어느순간 최종 weight 값들이 inf (무한대)로 뜨기 시작한다.
activation function을 쓰면 극단적인 weight 변화라는 문제를 해결할 수 있지만, Error를 weight 값에 반영해 주는 방법을 바꿔주어야 한다.
여기서부터가 가장 어려운 개념이다.
Partial Derivative (편미분)과 Error
최대한 쉽게 설명하려고 노력하겠다.
우리가 결국 Perceptron을 만들면서 궁극적으로 원하는 것은 단 하나다.
Weight 값을 변화, 즉 증가시키거나 감소시켜서 Error를 줄이는 것
"변화" 라는 단어만 나오면 수학에서 바로 튀어 나오는 것이 바로 미분이다.
대체로 미분을 배울때 미분을 계산하는 부분에 많은 시간을 써서 그런지 미분이 의미하는 것을 잊는 경우가 있다.
특정 함수 f(x)를 미분해서 새로운 함수 f'(x)를 만들고, x에 특정한 값, 예를들어 3, 을 넣어주면 f(x) 함수의 숫자 3에서의 기울기를 알려준다.
f'(3)이 양수이면, f(3)인 지점에서 기울기가 오른쪽으로 증가한다는 뜻이니, f(3+아주 작은 수)의 값이 f(3)보다 클 것이다.
반대로 음수이면, f(3+아주 작은 수)의 값이 f(3)보다 작을 것이다.
만약에, X축이 weight, Y축이 Error인 아래의 좌측과 같은 그래프가 있다면 가장 적절한 weight 값은 어디일까?

당연히 중심부근에 있는 Error가 가장 작아지는 지점이다.
하지만 이런 그래프를 쉽게 그릴 수 있었다면 고등학교 2학년 방학숙제로 알파고를 만드는 내용이 나갔을 것이다.
대신 만약에 오른쪽과 같이 특정 weight 지점에서 weight-Error 그래프의 기울기라도 알 수 있으면 어떨까?
위의 예처럼 그래프의 기울기가 양수라면, weight을 증가시키면 Error가 증가하니 weight 값을 살짝 감소시키면 적어도 지금보다는 Error가 작아질 것이라고 확신할 수 있다.
또한 weight 값을 얼마나 감소 시켜야 할지도 대략 알 수 있다.
아래의 그림 모두 미분값의 기울기가 음수라 weight을 증가시키는 것이 Error를 낮출 가능성이 높다.
어느 경우 weight를 더 많이 증가시켜야 할까?

좌측의 경우 weight이 커지면 슬슬 그래프가 평평해질 것 같다.
그에 비해서 우측의 경우는 신나게 아래로 내려가는 중인 것 같다.
이런 경우 우측의 경우 많이 weight 값을 증가시켜도 될 것 같지만, 좌측의 경우 너무 많이 weight 값을 증가시켰다가는 Error가 더 올라가버릴지도 모른다.
즉, weight은 Error를 weight로 미분한 값의 반대방향으로 움직어야 한다.
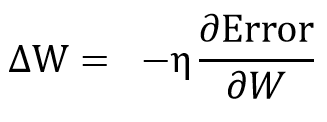
W의 변화량 = learning rate * (W에 대한 Error의 기울기) 의 반대
여기까지 이해가 되었다면 Error를 weight로 미분한 값만 알면 weight을 어떻게 바꿔야 할지 알 수 있다는 것을 눈치챘을 것이다.
기울기를 구하는 것이니 미분을 쓰면 될텐데, 편미분은 또 무슨 말일까?
편미분은 미분과 다른 것이 없다. 단지 미분을 하는데, 다른 변수는 다 무시해버리고 관심있는 변수로만 미분을 한다는 것이다.
예를들어 아래와 같은 수식이 있다고 하자.

함수 f는 x,y,z의 세 변수에 대한 복잡한 함수이다.
이를 x에 대해서 편미분을 하라는 것은 x 이외의 변수는 모두 상수로 보고 x에 대해서만 미분을 하면 된다.

참고로 편미분의 기호는 d 가 아닌 6을 거꾸로 쓴 듯한 기호로 표기한다.
편미분의 의미는 다른 변수들은 내 알 바 아니고 원하는 변수의 증감이 전체 함수의 기울기에 어떤 영향을 미치는지를 알려주는 것이다.
결론적으로 편미분 이야기를 꺼낸 이유는, weight의 변화에 따라 Error가 어떻게 달라지는지를 알기 위함, 즉, 아래의 값을 구하면 weight를 올릴지 내릴지 알 수 있다.
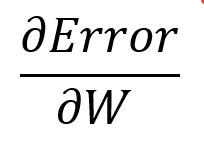
partial derivative의 또 다른 특성 중 하나는 chain rule 이다.
미분 가능한 함수들을 서로 연달아 배치해서 계산을 하는 방법인데, 수학적으로 말하자면 이 chain rule이 있기에 multi layer perceptron이 성립할 수 있다.

위와 같이 partial derivative 하나를 두 개로 쪼개서 계산할 수 있다.
그래서 SLP에 이를 적용해보자.
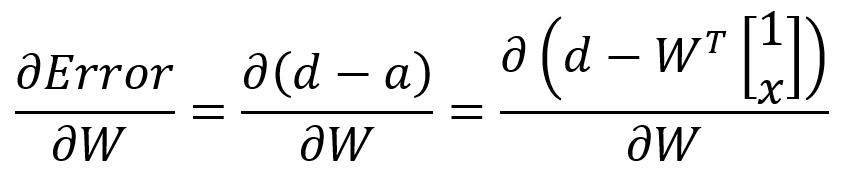
뭔가 이상하다.
저대로 가면 W가 있는 항이 우측 항 밖에 없으니 상수인 desired input은 W로 미분하면 사라진다.
Error function의 정의가 partial derivative 를 사용한 weight update방식에 맞지 않아서 그렇다.
desired output과 actual output의 차이의 제곱을 2로 나눈 것을 Error로 사용하기로 하면 문제가 해결된다.
어? 맘대로 Error function을 바꿔도 되나?
상관 없다. desired output과 actual output의 차이가 줄어들 수록 Error function의 값이 줄어들기만 하면 어떤 Error function을 써도 문제가 없다.
결과는 다음과 같다.

(d-a)는 Error, 그 뒤의 항은 input node의 값이다.
정확하게 우리가 위에서 본 식이다.
눈치챘을 수도 있지만 Error function 앞에 붙여둔 1/2는 정말 아무 의미없는 숫자다. (1/100 로 해도 된다.)
대신 1/2로 해두면 미분할 때 위에 있던 2가 똑 떨어져 나오기 때문에 위처럼 식이 깔끔해질 수 있다.
Single Layer Perceptron - with activation function
activation function은 input node와 각각의 weight 들의 곱의 합, 즉 a 값이 특정 범위 내에 있도록 해주는 함수이다.
가장 많이 사용하는 함수는 sigmoid, tanh, ReLU function 이며 output node의 값이 극단적으로 나오지 않도록 제한해주는 역할을 한다.

X 값에 따라 제한된 범위에서 Y값이 나오도록 하는 것 외에 activation function에는 한가지 요구사항이 붙는다.
바로 미분 가능성이다.
미분이 가능해야 나중에 partial derivative를 구할 수 있기에 위의 세 그래프 모두 X에 대해서 미분이 가능하다.
이 이후로 부터는 activation function으로 sigmoid 함수를 사용하도록 하겠다.

이 sigmoid 함수는 미분을 하면 재미있는 모습을 보여주는데, sigmoid 함수 y=f(x)는 미분을 하면 y(1-y) 로 표현이 된다.
미분하기 전 값으로 미분 후의 값을 표현할 수 있는 것이다.

위에서 언급한 tanh 함수도 미분을 하면 자기 자신으로 표현을 할 수 있으며, 이런 특성은 이후 아주 편리하다.
Feed Forward 계산
activation function이 없는 경우와 똑같다.
단지 node와 weight의 dot product를 바로 output으로 쓰는 것이 아니라 이 값을 activation function에 집어넣어서 나온 값을 output으로 사용한다.
아래에서 각 node의 weighted sum을 구한 뒤, sigmoid 함수에 넣어서 0.9598 이라는 값을 뽑아내는 것을 볼 수 있다.
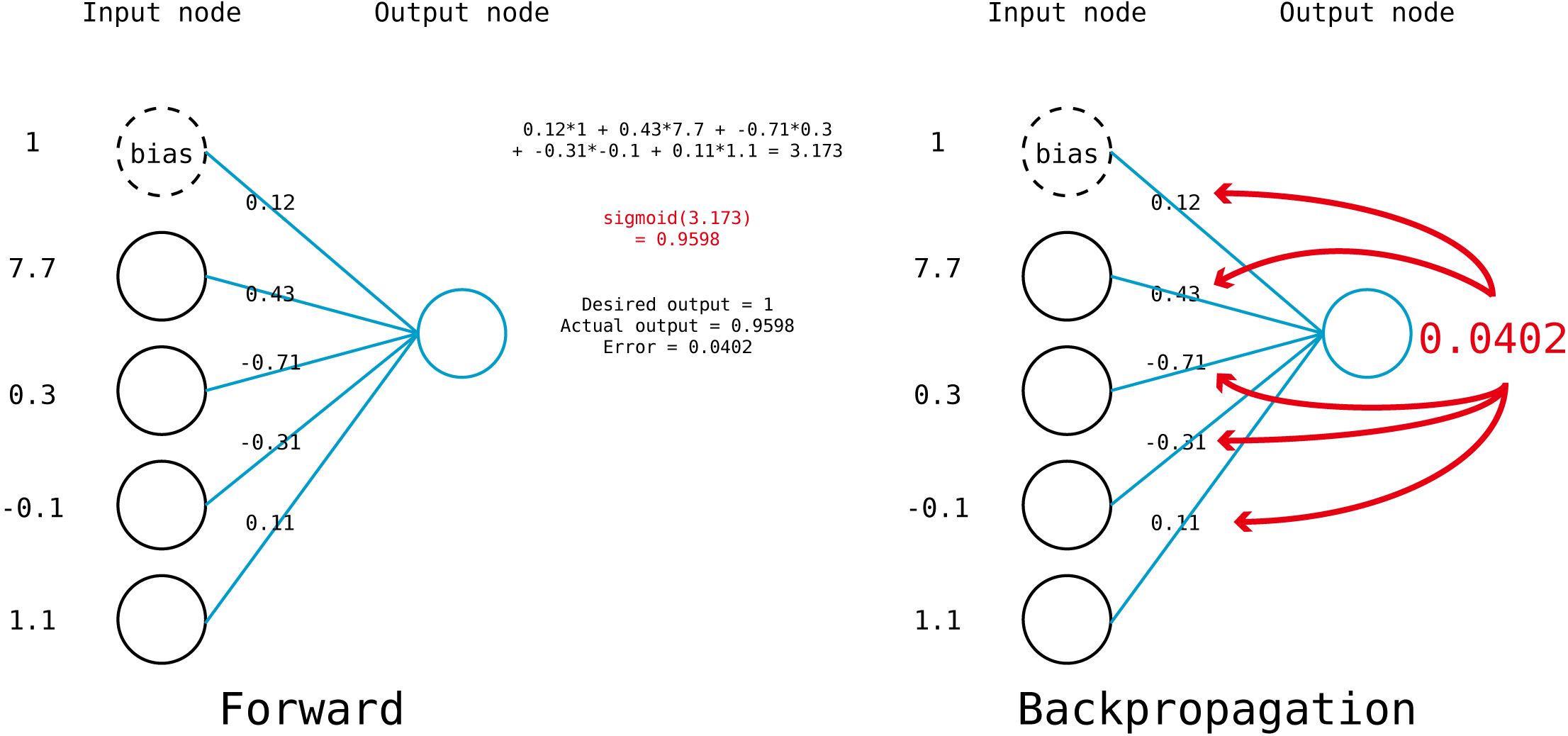
위에서 사용한 코드의 맨 아래 한 줄만 추가하면 feed forward 파트는 끝이다.
import numpy as np
# Constants
num_input_node = 4
num_output_node = 3
learning_rate = 0.1
num_epoch = 100
# Variables
weights = np.random.rand(num_input_node + 1, num_output_node) * 2 -1
# rand 함수는 0~1 사이 값을 주기에 x2-1을 하면 -1과 1 사이의 값이 나온다.
# Feed Forward
input_node = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)
##############################여기부터##############################################
output_node = 1 / (1+np.exp(a))Backpropagation 계산
위에서 언급한 partial derivative를 쓰면 Error에 대한 weight의 영향을 아래처럼 계산할 수 있다.
참고로 a는 input node에 각각 해당하는 weight 값을 곱하고 합한 값
y는 이 a를 activation function을 통과한 값이다.
x에 weight을 곱하고 합하기(=a). 이 결과를 sigmoid 함수에 넣기(=y)

마지막 식을 차원에 맞춰서 정렬한 후, 코드로 바꾸면 아래와 같다.
import numpy as np
# Constants
num_input_node = 4
num_output_node = 3
learning_rate = 0.1
num_epoch = 100
# Variables
weights = np.random.rand(num_input_node + 1, num_output_node) * 2 -1
# rand 함수는 0~1 사이 값을 주기에 x2-1을 하면 -1과 1 사이의 값이 나온다.
# Feed Forward
input_node = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)
output_node = 1 / (1+np.exp(a))
##############################여기부터##############################################
# Backpropagation
delta = -(desired_output - output_node) * output_node * (1-output_node)
new_weights = weights + learning_rate*( np.dot(delta, input_node.T).T )
코드 중간에 delta 라는 변수를 따로 만들고 나중에 bias를 포함한 input node의 값을 곱해주었다.
이를 반영해서 돌아가는 iris 코드는 다음과 같다.
import numpy as np
from sklearn import datasets
data = datasets.load_iris()
X = data.data
y = data.target
# Constants
num_input_node = 4
num_output_node = 3
learning_rate = 0.1
num_epoch = 1000
# Variables
weights = np.random.rand(num_input_node + 1, num_output_node) * 2 -1
# rand 함수는 0~1 사이 값을 주기에 x2-1을 하면 -1과 1 사이의 값이 나온다.
for epoch in range(num_epoch):
for sample,target in zip(X,y):
# Make input node to column vector
x = np.reshape(sample, [4, -1])
# Feed Forward
input_node = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)
output_node = 1 / (1 + np.exp(-a))
# Make desired output to column vector
desired_output = np.zeros([3,1])
desired_output[target] = 1
# Backpropagation
delta = -(desired_output - output_node) * output_node * (1-output_node)
new_weights = weights - learning_rate*( np.dot(delta, input_node.T).T)
weights = new_weights
score = 0
for sample,target in zip(X,y):
# Make input node to column vector
x = np.reshape(sample, [4, -1])
# Feed Forward
input_node = np.vstack([[[1]], x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a = np.dot(weights.T, input_node)
output_node = 1 / (1 + np.exp(-a))
score += int(np.argmax(output_node) == target)
print(score / len(X))Multi Layer Perceptron
편미분과 말도 안되는 선형대수를 뚫고 위 까지 이해를 했다면, MLP도 정말 쉽게 넘어갈 수 있다.
중간에 back propagation에 한 스텝이 추가될 뿐이다.
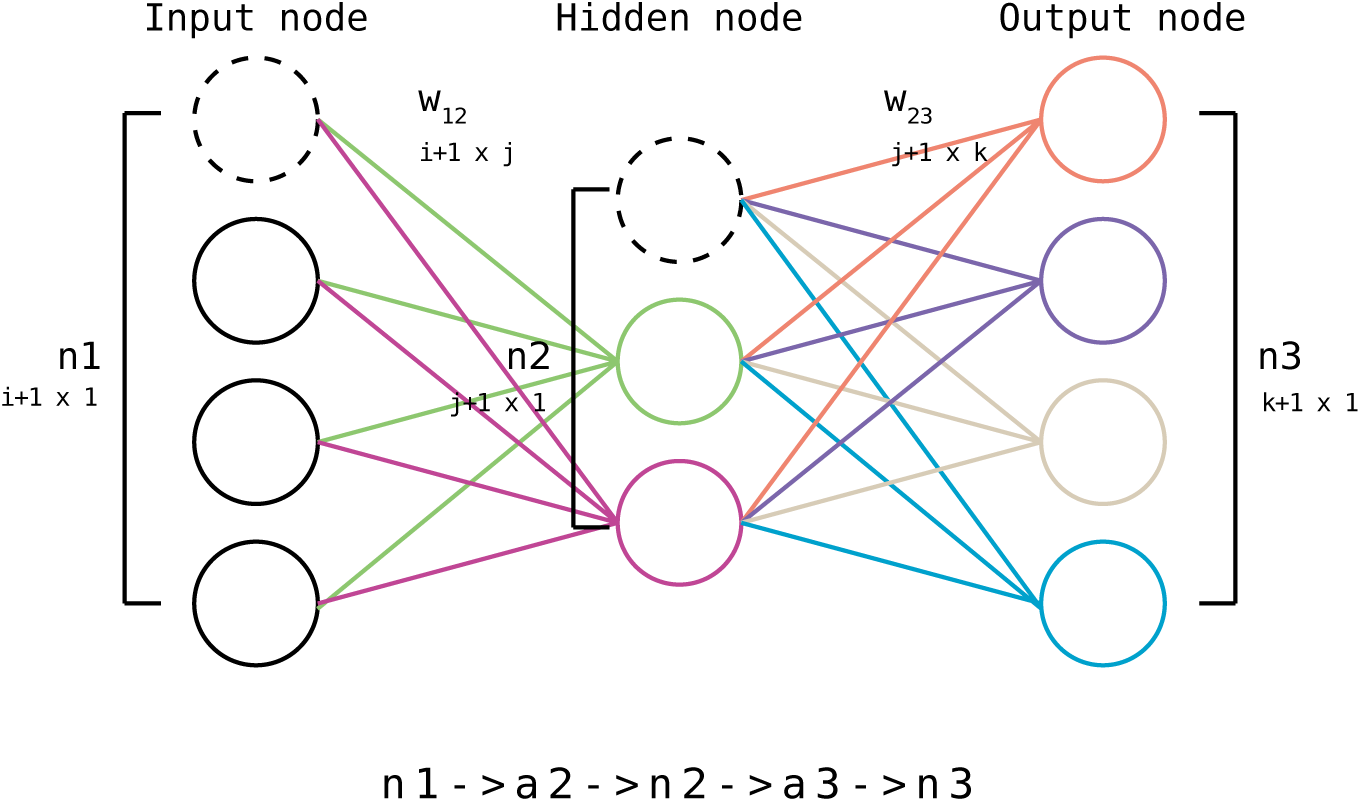
node가 총 3개가 되고 이에따라 weight matrix도 두개가 필요하다.
input, hidden, output으로 명명하면 혼돈의 여지가 있어서 순서대로 n1, n2, n3로 명명하고 weight 들은 첨자로 어느 노드 사이에 있는 weight 인지 달아두었다.

Feed Forward 계산
import numpy as np
# Constants
num_n1_node = 4
num_n2_node = 3
num_n3_node = 4
learning_rate = 0.1
num_epoch = 100
# Variables
W_12 = np.random.rand(num_n1_node + 1, num_n2_node) * 2 - 1
W_23 = np.random.rand(num_n2_node + 1, num_n3_node) * 2 - 1
# Feed Forward
n1 = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a2 = np.dot(W_12.T, n1)
n2 = 1 / (1 + np.exp(-(a2)))
n2 = np.vstack(([[1]], n2))
a3 = np.dot(W_23.T, n2)
n3 = 1 / (1 + np.exp(-(a3)))
Backpropagation 계산
W23의 계산

W23은 output node인 n3와 직접 연결되어 있기에 Single Layer 처럼 구하면 된다.
문자들만 달라졌지 위에서 작성한 식과 똑같다.
W12의 계산
W23의 경우는 바로 output node와 연결이 되어 있어서 어느 부분을 고치면 되는지 직관적으로 알 수 있는데, W12의 영향력은 W23을 한번 더 지나서 나타나기에 중간 연결고리를 모른다.
대신 우리는 각각의 값들의 아래의 연결고리를 안다.

a2랑 W12가 같이 있는 식이 있고, a2 & n2 | n2 & a3 | a3 & n3 | Error 와 n3가 같이 있는 식도 알고 있다.
따라서 이러한 연결구조를 활용해서 chain rule을 통해 아래의 식을 구할 수 있다.
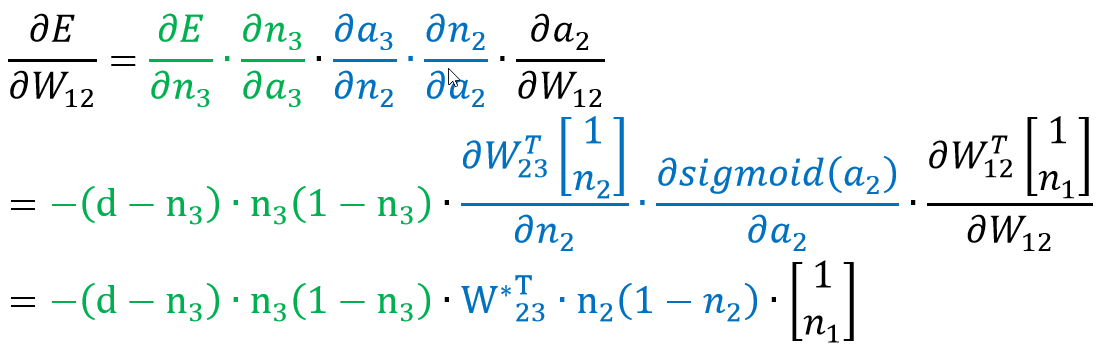
마지막 식의 첫 파란 항에서 W23 위에 *이 붙어있는데, 이는 첫째행을 제외한 W23을 말한다.
이 행을 지워주는 이유는 두 가지 방법으로 설명할 수 있는데,
일단, 편미분을 bias를 포함한 n2로 하는 것이 아니라 n2로만 하기에 Weight에서 bias 관련 부분을 빼고 나머지 값만 써주는 것이라고 설명할 수 있다.
다른 방법으로는 W23의 첫째 행에는 n2의 bias와 n3를 연결하는 weight 값이 들어있는데, n1과 n2의 bias는 서로 연결되어 있지 않으므로 n2의 bias 관련 정보는 빼주는 것이라고도 설명할 수 있다.

겨우 끝났다.
이 모든 과정을 코드로 정리하면 아래와 같다.
import numpy as np
# Constants
num_n1_node = 4
num_n2_node = 3
num_n3_node = 4
learning_rate = 0.1
num_epoch = 100
# Variables
W_12 = np.random.rand(num_n1_node + 1, num_n2_node) * 2 - 1
W_23 = np.random.rand(num_n2_node + 1, num_n3_node) * 2 - 1
# Feed Forward
n1 = np.vstack([[[1]],x]) # input vector x 위에 bias를 위한 원소 1을 추가해준다.
a2 = np.dot(W_12.T, n1)
n2 = 1 / (1 + np.exp(-(a2)))
n2 = np.vstack(([[1]], n2))
a3 = np.dot(W_23.T, n2)
n3 = 1 / (1 + np.exp(-(a3)))
##############################여기부터##############################################
# Backpropagation
delta23 = -(desired_output - n3) * n3 * (1-n3)
W_23 = W_23 - learning_rate * np.dot(delta_23, n2.T).T
# 위에서 n2 변수를 bias를 포함해서 정의했기에 여기서는 [1:,:] 인덱싱을 사용해 맨 윗행 값을 뺀다.
# 또한 W_23에서도 맨 윗행 값을 뺀다.
delta_12 = np.dot(W_23[1:, :], delta_23) * n2[1:, :] * (1 - n2[1:, :])
W_12 = W_12 - learning_rate * np.dot(delta_12, n1.T).T
iris 데이터에 적용한 코드는 아래와 같다.
import numpy as np
from sklearn import datasets
from sklearn import model_selection
data = datasets.load_iris()
X = data.data
y = data.target
# Select node
num_n1_node = 4
num_n2_node = 12
num_n3_node = 3
# Generate model
W_12 = np.random.rand(num_n1_node + 1, num_n2_node) * 2 - 1
W_23 = np.random.rand(num_n2_node + 1, num_n3_node) * 2 - 1
num_epoch = 1000
learning_rate = 0.2
for epoch in range(num_epoch):
for sample, target in zip(X,y):
# Forward
n1 = np.reshape(np.append([1], sample), [num_n1_node + 1, -1])
a2 = np.dot(W_12.T, n1)
n2 = 1 / (1 + np.exp(-(a2)))
n2 = np.vstack(([[1]], n2))
a3 = np.dot(W_23.T, n2)
n3 = 1 / (1 + np.exp(-(a3)))
# Backward
DesiredOutput = np.zeros([num_n3_node, 1])
DesiredOutput[target] = 1
Error = 0.5 * (DesiredOutput - n3) ** 2
delta_23 = -(DesiredOutput - n3) * n3 * (1 - n3)
W_23 = W_23 - learning_rate * np.dot(delta_23, n2.T).T
delta_12 = np.dot(W_23[1:, :], delta_23) * n2[1:, :] * (1 - n2[1:, :])
W_12 = W_12 - learning_rate * np.dot(delta_12, n1.T).T
score = 0
for sample, target in zip(X,y):
n1 = np.reshape(np.append([1], sample), [num_n1_node + 1, -1])
y1 = np.dot(W_12.T, n1)
n2 = 1 / (1 + np.exp(-(y1)))
n2 = np.vstack(([[1]], n2))
y2 = np.dot(W_23.T, n2)
n3 = 1 / (1 + np.exp(-(y2)))
score += int(np.argmax(n3) == target)
print(score / len(X))아직 이것보다 더 쉽게 Multi Layer Perceptron을 설명하는 글을 보지 못했다.
Multi layer를 도입하기 위해서는 partial derivative 개념은 필수이며, 2차원 weight matrix에 대한 연산을 설명하기 위해서는 Sigma로 도배하거나, 선형대수로 머리를 터뜨려야 한다.
그나마 선형대수를 사용하는 것이 겉으로 보기에 아주 깔끔하고 정돈되어 있어서 굳이 이 방법을 사용했다.
하나 고백하자면 matrix와 matrix의 partial derivative는 제대로 정의가 되어있지 않다고 한다. (wiki 참고)
따라서 matrix calculus를 제대로 배운 사람이라면 말도 안되는 transpose, 맘대로 어기는 Commutative property에 혀를 찰 것이며 제대로 계산을 하기 위해서는 다른 방법을 써주어야 하는 것 같다.
matrix calculus 부분은 다음을 위한 과제로 남겨두려고 한다.
어찌되었건, dimension만 제대로 맞춰주면 위의 코드는 돌아간다!
마치며
기계학습에 대한 대중들의 관심이 높아져서 그런지 관련 사기꾼들도 같이 늘어나는 것 같다.
내 연구 프로젝트에 대해서 생뚱맞게 4차 산업혁명이나 인공지능과 관련있는 점이 있냐고 물어보는 사람들이 있는가 하면, 기계학습과 인공지능의 차이도 모르는 사람들이 아무곳에나 "자율형", "인공지능" 등의 말을 붙이고 다닌다.
물론, 어떠한 학문이든 진입 장벽은 낮을수록 좋고, 누구나 쉽게 분야에 참여해 배워보고, 그 유용성을 누려야 한다고 생각한다.
하지만 가상악기와 MIDI를 사용해서 바이올린을 연주하는 사람이 "나는 바이올린을 잘 안다!" 라고 말하면 안되듯이 남이 만들어 놓은 코드 몇 줄로 classifier를 만들고 기계학습을 잘한다고 말하면 안된다.
더욱이 기계학습을 연구에 사용하거나, 실무에 사용하는 경우 적어도 기저 개념을 한번이라도 유도해보지 않으면 주의점과 한계들을 놓쳐서 치명적인 오류를 범할 수 있을 것이다.
자신과 관련된 분야에 대중의 관심이 많아질 수록, 보다 겸손하고 신중한 자세를 취하는 것이 옳은 것 같다.
- 부족한 글 읽어주셔서 감사합니다.
- 오류나 오타가 있으면 댓글로 감사히 받겠습니다.
'취미 > Programming' 카테고리의 다른 글
| [Vim] Linux 상에서의 Not an editor command: ^M 문제 (0) | 2021.03.24 |
|---|---|
| Python(anaconda) Vim intagration (2) | 2020.10.28 |
| [GitHub] 3. GUI Git: GitHub Desktop, Sourcetree, GitKraken (0) | 2019.11.13 |
| [GitHub] 2. git과 GitHub의 관계 (0) | 2019.11.12 |
| [GitHub] 1. 시작하기 (0) | 2019.11.11 |